题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且asinB-bcosC=ccosB.(Ⅰ)判断△ABC的形状;
(Ⅱ)若f(x)=sinx+cosx,求f(A)的最大值.
【答案】分析:(I)法一:由已知结合正弦定理对已知化简可求B,进而可判断三角形的形状
法二:由已知结合余弦定理对已知化简可求B,进而可判断三角形的形状
(II)由辅助角公式对已知函数f(x)先化简,然后代入可求f(A),结合(I)中的角B可求A的 范围,然后结合正弦函数的性质即可求解
解答:解:(Ⅰ)(法1)因为 asinB-bcosC=ccosB,
由正弦定理可得 sinAsinB-sinBcosC=sinCcosB. …(3分)
即sinAsinB=sinCcosB+cosCsinB,
所以 sin(C+B)=sinAsinB. …(4分)
因为在△ABC中,A+B+C=π,
所以 sinA=sinAsinB又sinA≠0,…(5分)
所以 sinB=1,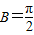 .
.
所以△ABC为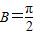 的直角三角形. …(6分)
的直角三角形. …(6分)
(法2)因为 asinB-bcosC=ccosB,
由余弦定理可得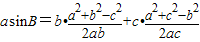 ,…(4分)
,…(4分)
所以 asinB=a.
因为a≠0,所以sinB=1. …(5分)
所以在△ABC中,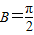 .
.
所以△ABC为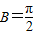 的直角三角形. …(6分)
的直角三角形. …(6分)
(Ⅱ)因为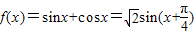 ,…(8分)
,…(8分)
所以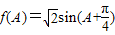 . …(9分)
. …(9分)
因为△ABC是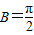 的直角三角形,
的直角三角形,
所以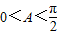 ,…(10分)
,…(10分)
所以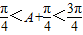 ,…(11分)
,…(11分)
所以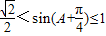 . …(12分)
. …(12分)
即f(A)的最大值为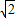 . …(13分)
. …(13分)
点评:本题主要考查了正弦定理、余弦定理及和差角公式在求解三角形中的应用,其中正弦函数性质的灵活应用是求解(II)的关键
法二:由已知结合余弦定理对已知化简可求B,进而可判断三角形的形状
(II)由辅助角公式对已知函数f(x)先化简,然后代入可求f(A),结合(I)中的角B可求A的 范围,然后结合正弦函数的性质即可求解
解答:解:(Ⅰ)(法1)因为 asinB-bcosC=ccosB,
由正弦定理可得 sinAsinB-sinBcosC=sinCcosB. …(3分)
即sinAsinB=sinCcosB+cosCsinB,
所以 sin(C+B)=sinAsinB. …(4分)
因为在△ABC中,A+B+C=π,
所以 sinA=sinAsinB又sinA≠0,…(5分)
所以 sinB=1,
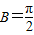 .
.所以△ABC为
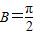 的直角三角形. …(6分)
的直角三角形. …(6分)(法2)因为 asinB-bcosC=ccosB,
由余弦定理可得
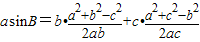 ,…(4分)
,…(4分)所以 asinB=a.
因为a≠0,所以sinB=1. …(5分)
所以在△ABC中,
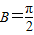 .
.所以△ABC为
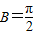 的直角三角形. …(6分)
的直角三角形. …(6分)(Ⅱ)因为
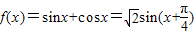 ,…(8分)
,…(8分)所以
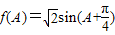 . …(9分)
. …(9分)因为△ABC是
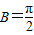 的直角三角形,
的直角三角形,所以
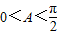 ,…(10分)
,…(10分)所以
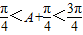 ,…(11分)
,…(11分)所以
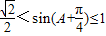 . …(12分)
. …(12分)即f(A)的最大值为
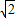 . …(13分)
. …(13分)点评:本题主要考查了正弦定理、余弦定理及和差角公式在求解三角形中的应用,其中正弦函数性质的灵活应用是求解(II)的关键

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |