题目内容
椭圆
上的一点
，它到椭圆的一个焦点
的距离是7，则它到另一个焦点
的距离是（ ）
上的一点，它到椭圆的一个焦点的距离是7，则它到另一个焦点的距离是（ ）A． | B． | C．12 | D．5 |
D
试题分析：先根据条件椭圆方程
求出a=6；再根据椭圆定义得到关于所求距离d的等式即可得到结论。设所求距离为d，由题得：a=6．根据椭圆的定义得：2a=7+d⇒d=2a-7=54．故可知d=5，那么故选D．
点评：解决涉及到圆锥曲线上的点与焦点之间的关系的问题中，圆锥曲线的定义往往是解题的突破口。
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
上的一个动点，过点P作PD垂直于
轴，垂足为D，Q为线段PD的中点。
则 ( ) 
与
顶点相同.
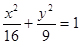的两个焦点，过F2的直线交椭圆于点A、B，若
,
（ ） 
(
)
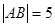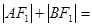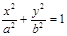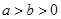，M,N是椭圆上关于原点对称的两点，P是椭圆上任意一点，且直线PM,PN的斜率分别为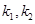
，
=
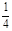，则椭圆的离心率为（ ）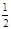
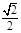
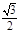
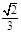
,在平面直角坐标系中,已知向量
,向量
,
,动点
的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状．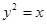
的准线方程是 
是双曲线C：
的左焦点，
是双曲线的虚轴，
是
的中点，过
的直线交双曲线C于
，且
,则双曲线C离心率是____