题目内容
 如图,已知正方形ABCD在直线MN的上方,边BC在直线MN上,E是线段BC上一点,以AE为边在直线MN的上方作正方形AEFG,其中AE=2,记∠FEN=α,△EFC的面积为S.
如图,已知正方形ABCD在直线MN的上方,边BC在直线MN上,E是线段BC上一点,以AE为边在直线MN的上方作正方形AEFG,其中AE=2,记∠FEN=α,△EFC的面积为S.(Ⅰ)求S与α之间的函数关系;
(Ⅱ)当角α取何值时S最大?并求S的最大值.
分析:(Ⅰ)观察图形知,EF=2,∠EAB=∠FEH=α,可将EC用α表示出来,再由三角形的面积公式
absinC建立S与α之间的函数关系;
(Ⅱ)由(I)得S=2sinαcosα-2sin2α,其中0≤α≤
,对函数的解析式进行化简,再求三角函数的最值即可得到S的最大值
| 1 |
| 2 |
(Ⅱ)由(I)得S=2sinαcosα-2sin2α,其中0≤α≤
| π |
| 4 |
解答: 解:(Ⅰ)过点F作FH⊥MN,H为垂足
解:(Ⅰ)过点F作FH⊥MN,H为垂足
由三角知识可证明∠EAB=∠FEH=α,FH=BE…2 分
在Rt△ABE中,EB=AEsinα=2sinα,BC=AB=AEcosα=2cosα
所以EC=BC-EB=2cosα-2sinα…4 分
所以△FCE的面积
S=
(2cosα-2sinα)•2sinα=2sinαcosα-2sin2α,其中0≤α≤
…(6分)
(Ⅱ)由(Ⅰ)可知S=2sinαcosα-2sin2α=sin2α+cos2α-1=
sin(2α+
)-1…(9分)
由0≤α≤
,得
≤2α+
≤
π,
∴当2α+
=
π,即α=
时,S最大=
-1…(11分)
因此,当α=
时,△EFC的面积S最大,最大面积为
-1. …12 分
 解:(Ⅰ)过点F作FH⊥MN,H为垂足
解:(Ⅰ)过点F作FH⊥MN,H为垂足由三角知识可证明∠EAB=∠FEH=α,FH=BE…2 分
在Rt△ABE中,EB=AEsinα=2sinα,BC=AB=AEcosα=2cosα
所以EC=BC-EB=2cosα-2sinα…4 分
所以△FCE的面积
S=
| 1 |
| 2 |
| π |
| 4 |
(Ⅱ)由(Ⅰ)可知S=2sinαcosα-2sin2α=sin2α+cos2α-1=
| 2 |
| π |
| 4 |
由0≤α≤
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
∴当2α+
| π |
| 4 |
| 1 |
| 2 |
| π |
| 8 |
| 2 |
因此,当α=
| π |
| 8 |
| 2 |
点评:本题考查已知三角函数的模型的应用问题,解题的关键是根据所研究的问题及图形建立三角函数关系,再利用三角函数的知识求最值,得出实际问题的解,本题第二小问求面积的最值,利用到了三角函数有界性,本题考查了函数的思想及转化的思想,本题运算量较大,计算时要严谨.

练习册系列答案
相关题目
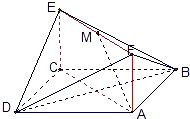 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.