题目内容
在
中,
分别是角
的对边长．已知a=2，
．
（1）若
，求
的值； （2）若的面积
，求
，
的值．
中,分别是角的对边长．已知a=2，．（1）若
，求的值； （2）若的面积，求，的值．(1) 
.
(2) c=5.
.
. (2) c=5.
.(1)本小题是已知两边及一边对角，解三角形的问题.可使用正弦定理.
（2）根据面积公式可先求出c,然后再利用余弦定理求出b.
(1) ∵cosB=
>0，且0<B<π，∴sinB=
. …………2分
由正弦定理得
， . ………………6分
(2) ∵S△ABC=
acsinB=4， ……………………………………………………8分
∴
， ∴c="5." …………………………………………………10分
由余弦定理得b2=a2+c2－2accosB，
∴
.
（2）根据面积公式可先求出c,然后再利用余弦定理求出b.
(1) ∵cosB=
>0，且0<B<π，∴sinB=. …………2分由正弦定理得
， . ………………6分(2) ∵S△ABC=
acsinB=4， ……………………………………………………8分∴
， ∴c="5." …………………………………………………10分由余弦定理得b2=a2+c2－2accosB，
∴
.
练习册系列答案
教材全解字词句篇系列答案
相关题目
中，角A、B、C的对边分别为a，b，c。角A，B，C成等差数列。
的值；
的值。
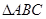中，角
、
、
的对边分别是
，
，
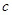，已知
．
，求
方向300
的海面P处，并以
的速度向西偏北
方向移动。台风侵袭的范围为圆形区域，当前半径为60
的速度不断增大，问几时后该城市开始受到台风的侵袭？
中，角
所对的边分别为
已知
且
．
时，求
的值；
为锐角，求
的取值范围．
，且C=60°，则ab的值为
B．
C． 1 D．
则△ABC的面积为（ ）
的取值范围是________. 
，3）
，3）
，3）