Question

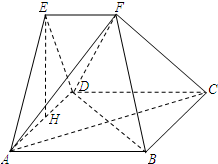如图，在多面体ABCD-EF中，四边形ABCD为正方形，EF∥AB，EF⊥EA，AB=2EF，∠AED=90°，AE=ED，H为AD的中点．
（Ⅰ）求证：EH∥平面FAC；
（Ⅱ）求证：EH⊥平面ABCD；
（Ⅲ）求二面角A-FC-B的大小．

Answer 1

分析：（Ⅰ）证明线面平行，只需证明EH平行于平面FAC中的一条直线，设AC∩BD=O，连接HO，FO，证明EH∥FO即可；
（Ⅱ）证明线面垂直，只需证明EH垂直于平面ABCD内的两条相交直线，利用证明AB⊥平面AED，即可证得；
（Ⅲ）根据AC，BD，OF两两垂直，建立空间直角坐标系，求出平面BCF的法向量、平面AFC的法向量，利用向量的夹角公式，即可求二面角A-FC-B的大小．

解答：（Ⅰ）证明：AC∩BD=O，连接HO，FO
因为ABCD为正方形，所以O是AC中点，
又H是AD中点，
所以OH∥CD ， OH=

1

2

CD，EF∥AB ， EF=

1

2

AB，
所以EF∥OH且EF=OH，
所以四边形EHOF为平行四边形，
所以EH∥FO，
又因为FO?平面FAC，EH?平面FAC．
所以EH∥平面FAC．…（4分）
（Ⅱ）证明：因为AE=ED，H是AD的中点，所以EH⊥AD…（6分）
又因为AB∥EF，EF⊥EA，所以AB⊥EA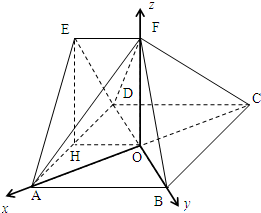
又因为AB⊥AD，所以AB⊥平面AED，
因为EH?平面AED，所以AB⊥EH，…（8分）
所以EH⊥平面ABCD．…（9分）
（Ⅲ）解：AC，BD，OF两两垂直，建立如图所示的坐标系，设EF=1，则AB=2，B(0，

2

，0)，C(-

2

，0，0)，F（0，0，1）…（10分）
设平面BCF的法向量为

n1

=(x，y，z)，

BC

=(-

2

，-

2

，0)，  

CF

=(

2

，0，1)，

n1

•

BC

=0，

n1

•

CF

=0
所以 

n1

=(-1，1，

2

)…（11分）
平面AFC的法向量为

n2

=(0，1，0)…（12分）cos＜

n1

，

n2

＞=

n1 • n2

| n1 |•| n2 |

=

1

2

．                       …（13分）
二面角A-FC-B为锐角，所以二面角A-FC-B等于

π

3

．…（14分）

点评：本题考查线面平行、线面垂直，考查面面角，解题的关键是熟练运用线面平行与垂直的判定，掌握求平面法向量的方法．