题目内容
如图,正方体ABCD—A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.

(1)求GH长的取值范围;
(2)当GH取得最小值时,求证:EH与FG共面;并求出此时EH与FG的交点P到直线 的距离.
的距离.

(1)求GH长的取值范围;
(2)当GH取得最小值时,求证:EH与FG共面;并求出此时EH与FG的交点P到直线
 的距离.
的距离. (1)[2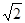 ,4] (2)
,4] (2)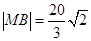
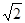 ,4] (2)
,4] (2)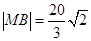
试题分析:解:(1)以D为原点,DA,DC,DD1分别为x轴,y轴,z轴建立空间直角坐标系.
设DG=a,DH=b,则E(4,0,4),F(0,4,4),G(a,0,0),H(0,b,0).
∴
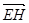 =(-4,b,-4),
=(-4,b,-4),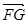 =(a,-4,-4).
=(a,-4,-4).∵EH⊥FG.
∴
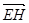 ·
·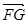 =-4a-4b+16=0,则a+b=4,即b=4-a.
=-4a-4b+16=0,则a+b=4,即b=4-a.又G1H在棱DA,DC上,则0≤a≤8,0≤b≤8,从而0≤a≤4.
∴GH=
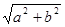 =
=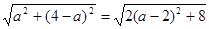 .
.∴GH取值范围是[2
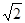 ,4] . ……6分
,4] . ……6分(2)当GH=2
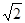 时,a=2,b=2.
时,a=2,b=2.∴
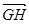 =(-2,2,0),
=(-2,2,0),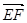 =(-4,4,0),即
=(-4,4,0),即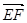 =2
=2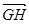 .
.∴EF∥GH,即EH与FG共面.
所以EF=2GH,EF∥GH,则
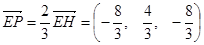 .
.设P(x1,y1,z1),则
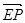 =(x1-4,y,z1-4).
=(x1-4,y,z1-4).∴x1=
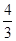 ,y1=
,y1=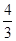 ,z1=
,z1=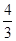 ,即P(
,即P(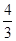 ,
,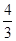 ,
,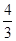 ).
).则P(
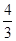 ,
,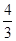 ,
,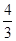 )在底面上ABCD上的射影为M(
)在底面上ABCD上的射影为M(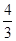 ,
,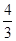 ,0).又B(8,8,0),
,0).又B(8,8,0),所以
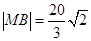 为点P到直线
为点P到直线 的距离. ……12分
的距离. ……12分
点评:关键是通过建立空间直角坐标系,然后表示点的坐标以及点在平面的射影得到距离,属于基础题。

练习册系列答案
相关题目
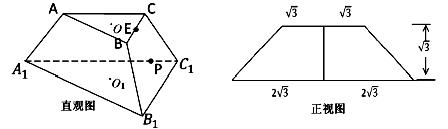
 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )




 中,若AB=2,
中,若AB=2, 则点A到平面
则点A到平面 的距离为( )
的距离为( ) 



 是直线,
是直线, 是两个不同的平面,下列命题成立的是( )
是两个不同的平面,下列命题成立的是( ) ,则
,则
 ∥
∥ ,则
,则 ,
, , 则
, 则
 和
和 及平面
及平面 ,则直线
,则直线 的一个充分条件是 ( )
的一个充分条件是 ( ) 且
且
 且
且

