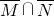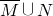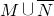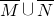Question

15、设全集为R，f （x）=sinx，g （x）=cosx，M={x|f （x）≠0}，N={x|g （x）≠0}，那么集合
{x|f （x）g （x）=0}等于（　　）

• A、

  .

  M

  ∩

  .

  N

• B、

  .

  M

  ∪N
• C、M∪

  .

  N

• D、

  .

  M

  ∪

  .

  N

Answer 1

分析：由f （x）g （x）=0可知f （x）=0或g （x）=0，所以{x|f （x）g （x）=0}={x|f （x）=0}∪{x|g （x）=0}．
而{x|f （x）=0}与M互为补集关系，则可选出答案．注意区分“或”与“且”．

解答：解：{x|f （x）g （x）=0}={x|f （x）=0或g （x）=0}={x|f （x）=0}∪{x|g （x）=0}，
故选D

点评：本题考查集合的基本运算，较简单．注意区分“或”与“且”的含义．