题目内容
已知抛物线y2=2px(p＞0)的一条焦点弦AB被焦点F分成m、n两部分，求证：
为定值，本题若推广到椭圆、双曲线，你能得到什么结论？
解析：（1）当AB⊥x轴时，m=n=p，
∴=
.
（2）当AB不垂直于x轴时，设AB:y=k(x-
),
A(x1,y1),B(x2,y2),|AF|=m,|BF|=n,
∴m=
+x1,n=
+x2.
将AB方程代入抛物线方程，得
k2x2-(k2p+2p)x+
=0,
∴
∴
=
=
.
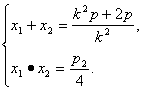
本题若推广到椭圆，则有
=
（e是椭圆的离心率）；若推广到双曲线，则要求弦AB与双曲线交于同一支，此时，同样有
=
(e为双曲线的离心率).
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目