题目内容
设n∈N*，n＞1，用数学归纳法证明：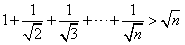
。
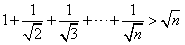。 证明：记
（n∈N*，n＞1），
（1）当n=2时，
，不等式成立；
（2）假设n=k（k∈N*，k≥2）时，不等式成立，
即
，
则当n=k+1时，
有
，
∴当n=k+1时，不等式也成立；
综合（1），（2）知，原不等式对任意的n∈N*（n＞1）都成立。
（n∈N*，n＞1），（1）当n=2时，
，不等式成立；（2）假设n=k（k∈N*，k≥2）时，不等式成立，
即
，则当n=k+1时，
有
，∴当n=k+1时，不等式也成立；
综合（1），（2）知，原不等式对任意的n∈N*（n＞1）都成立。
练习册系列答案
相关题目
+
+
．
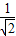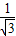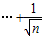
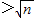