题目内容
已知点A(2,0),B(0,2),C(cosα,sinα),且0<α<π.
(1)若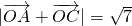 ,求角α;
,求角α;
(2)若 ,求cosα-sinα的值.
,求cosα-sinα的值.
解:(1)∵点A(2,0),B(0,2),C(cosα,sinα),
∴ ,
,
∴ ,
,
∵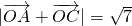 ,
,
∴(2+cosα)2+sin2α=7
∴cosα=
∵0<α<π.
∴α= ;
;
(2)∵点A(2,0),B(0,2),C(cosα,sinα),
∴
∵ ,
,
∴(cosα-2)cosα+sinα(sinα-2)=0
∴
两边平方得:
∴
∴
∵ ,0<α<π
,0<α<π
∴sinα>0,cosα<0
∴cosα-sinα=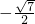 .
.
分析:(1)分别表示 ,再利用
,再利用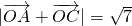 ,即可求得角α;
,即可求得角α;
(2)用坐标表示向量,利用向量垂直,得到数量积为0,进而可求cosα-sinα的值.
点评:本题以向量为载体,考查三角函数,解题的关键是用坐标表示向量,正确运用同角三角函数的关系.
∴
 ,
,∴
 ,
,∵
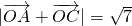 ,
,∴(2+cosα)2+sin2α=7
∴cosα=

∵0<α<π.
∴α=
 ;
;(2)∵点A(2,0),B(0,2),C(cosα,sinα),
∴

∵
 ,
,∴(cosα-2)cosα+sinα(sinα-2)=0
∴

两边平方得:

∴

∴

∵
 ,0<α<π
,0<α<π∴sinα>0,cosα<0
∴cosα-sinα=
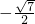 .
.分析:(1)分别表示
 ,再利用
,再利用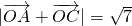 ,即可求得角α;
,即可求得角α;(2)用坐标表示向量,利用向量垂直,得到数量积为0,进而可求cosα-sinα的值.
点评:本题以向量为载体,考查三角函数,解题的关键是用坐标表示向量,正确运用同角三角函数的关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目