题目内容
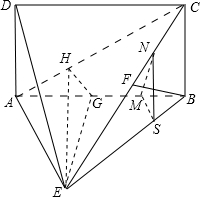 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.(1)设M,N分别在线段AB,EC上,且满足AM=2MB,EN=2NC,求证:MN∥平面DAE;
(2)求证:AE⊥BE;
(3)求二面角E-AC-B的大小.
分析:(1)在EB上取点S,使ES=2SB,利用平行线截线段成比例得到线线平行,从而得到线面平行,再得到面面平行,最终得到线面平行;
(2)证明AE⊥EB,可先证明AE⊥平面EBC,要证AE⊥平面EBC,只要证AE⊥BC,AE⊥BF即可,由已知容易得到AE⊥BC,AE⊥BF,则问题得证;
(3)因为AE=EB,取AB中点G后得到EG⊥AB,过G作GH⊥AC于H,连结EH后即可得到∠EHG为要求二面角的平面角,通过解三角形求出EG和GH的长度,则二面角的正切值可求,利用反三角函数求出二面角的大小.
(2)证明AE⊥EB,可先证明AE⊥平面EBC,要证AE⊥平面EBC,只要证AE⊥BC,AE⊥BF即可,由已知容易得到AE⊥BC,AE⊥BF,则问题得证;
(3)因为AE=EB,取AB中点G后得到EG⊥AB,过G作GH⊥AC于H,连结EH后即可得到∠EHG为要求二面角的平面角,通过解三角形求出EG和GH的长度,则二面角的正切值可求,利用反三角函数求出二面角的大小.
解答: (1)证明:如图,在EB上取点S,使ES=2SB,连接MS,NS
(1)证明:如图,在EB上取点S,使ES=2SB,连接MS,NS
∵AM=2MB,EN=2NC,ES=2SB
∴NS∥BC,又BC∥AD,∴NS∥AD,AD?平面ADE,NS?平面ADE,∴NS∥平面ADE.
MS∥AE,AE?平面ADE,MS?平面ADE,∴MS∥平面ADE,又MS∩NS=S,
∴平面MNS∥平面ADE,
∴MN∥平面DAE;
(2)证明:∵AD⊥平面ABE,∴AD⊥AE,又∵AD∥BC,∴BC⊥AE,
由已知BF⊥平面ACE,∴BF⊥AE,而BC∩BE=B,∴AE⊥面BCE.
则AE⊥BE.
∵四边形ABCD为矩形,∴AD⊥AB,
(3)解:取AB中点G,连结EG,在平面ABCD中作GH⊥AC于H,连接EH
∵AE=EB,∴EG⊥AB,由AD⊥平面ABE,知面ABCD⊥面ABE,∴EG⊥面ABCD,
∴EG⊥AC,又GH⊥AC,EG∩GH=G,∴AC⊥EGH,则∠EHG为所求二面角的平面角.
在Rt△AEB中,AE=EB=2,易得到:AB=2
,EG=
AB=
.
在Rt△ABC中,AC=2
,由△AHG∽△ABC,可得
=
,∴HG=
=
=
.
∴在Rt△EGH中,tan∠EHG=
=
=
,∴∠EHG=60°.
 (1)证明:如图,在EB上取点S,使ES=2SB,连接MS,NS
(1)证明:如图,在EB上取点S,使ES=2SB,连接MS,NS∵AM=2MB,EN=2NC,ES=2SB
∴NS∥BC,又BC∥AD,∴NS∥AD,AD?平面ADE,NS?平面ADE,∴NS∥平面ADE.
MS∥AE,AE?平面ADE,MS?平面ADE,∴MS∥平面ADE,又MS∩NS=S,
∴平面MNS∥平面ADE,
∴MN∥平面DAE;
(2)证明:∵AD⊥平面ABE,∴AD⊥AE,又∵AD∥BC,∴BC⊥AE,
由已知BF⊥平面ACE,∴BF⊥AE,而BC∩BE=B,∴AE⊥面BCE.
则AE⊥BE.
∵四边形ABCD为矩形,∴AD⊥AB,
(3)解:取AB中点G,连结EG,在平面ABCD中作GH⊥AC于H,连接EH
∵AE=EB,∴EG⊥AB,由AD⊥平面ABE,知面ABCD⊥面ABE,∴EG⊥面ABCD,
∴EG⊥AC,又GH⊥AC,EG∩GH=G,∴AC⊥EGH,则∠EHG为所求二面角的平面角.
在Rt△AEB中,AE=EB=2,易得到:AB=2
| 2 |
| 1 |
| 2 |
| 2 |
在Rt△ABC中,AC=2
| 3 |
| GH |
| BC |
| AG |
| AC |
| AG•BC |
| AC |
| ||
2
|
| ||
| 3 |
∴在Rt△EGH中,tan∠EHG=
| EG |
| GH |
| ||||
|
| 3 |
点评:本题考查了直线与平面的平行直线与平面的垂直的判定,考查了二面角的平面角的求法,综合考查了学生的空间想象能力和思维能力,“寻找垂面,构造垂线”是找二面角的平面角最有效的方法,此题是中档题.

练习册系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=