题目内容
设椭圆ax2+by2=1与直线x+y=1相交于A、B两点,且|AB|=2
解:将椭圆方程与直线方程联立,消去y并整理得(a+b)x2-2bx+b-1=0.
设A(x1,y1)、B(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
∴|AB|=![]() |x1-x2|
|x1-x2|
=![]() ·
·![]()
=2·![]()
=![]() ,
,
y1+y2=1-x1+1-x2=2-(x1+x2)=![]() ,kOM=
,kOM= .
.
由题意知
解之,得
故所求椭圆方程为![]() +
+![]() y2=1.
y2=1.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 ,求椭圆的方程.
,求椭圆的方程.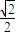 ,求椭圆的方程.
,求椭圆的方程.