题目内容
设抛物线y2=2px(p>0)的焦点为F,其准线与x轴交于点C,过点F作它的弦AB,若∠CBF=90°,则|AF|-|BF|=分析:先假设方程与抛物线方程联立,借助于求出点的坐标,从而求出线段长,进而求出|AF|-|BF|.
解答:解:设AB方程为:y=k(x-
)(假设k存在),与抛物线y2=2px(p>0)联立得k2(x2-px+
)=2px,
即k2x2-(k2+2)px+
=0
设两交点为A(x2,y2),B(x1,y1),∠CBF=90°即(x1-
)(x1+
)+y12=0,
∴x12+y12=
,∴x12+2px1-
=0,即(x1+p)2=
p2,解得x1=
p,
∴B(
p,
p),|BC|=
p,|BF|=
p,
∵x1x2=
,x1=
p,
∴x2=
p
∴A(
p,-
p),|AF|=
p,
∴|AF|-|BF|=2P,
故答案为2P.
| p |
| 2 |
| p2 |
| 4 |
即k2x2-(k2+2)px+
| (kp)2 |
| 4 |
设两交点为A(x2,y2),B(x1,y1),∠CBF=90°即(x1-
| p |
| 2 |
| p |
| 2 |
∴x12+y12=
| p2 |
| 4 |
| p2 |
| 4 |
| 5 |
| 4 |
-2+
| ||
| 2 |
∴B(
-2+
| ||
| 2 |
-2+
|
| ||||
| 2 |
-1+
| ||
| 2 |
∵x1x2=
| p2 |
| 4 |
-2+
| ||
| 2 |
∴x2=
2+
| ||
| 2 |
∴A(
2+
| ||
| 2 |
2+
|
3+
| ||
| 2 |
∴|AF|-|BF|=2P,
故答案为2P.
点评:直线与曲线相交问题,通常是联立方程组成方程组,从而可求相关问题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
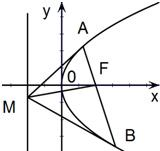 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)