题目内容
函数f（x）=2x2+2x+3，x∈[-1，1]的值域是 ．
【答案】分析：把此二次函数表示为顶点形式得到对称轴和顶点坐标，在[-1，1]上根据图象的特征求出最大值和最小值即可得到f（x）的值域．
解答：解：f（x）=2x2+2x+3=2（x+
）2+
为开口向上，顶点坐标为（-
，
），对称轴为直线x=-
的抛物线，
因为x∈[-1，1]，所以顶点能取到，则f（x）的最小值为
，
根据抛物线图象可知x=1时，f（x）max=f（1）=7．
所以函数f（x）的值域为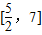
故答案为：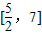
点评：本题主要考查学生会根据自变量的范围求二次函数所对应的值域，要求学生灵活运用二次函数的图象与性质求最值，属于基础题．
解答：解：f（x）=2x2+2x+3=2（x+
）2+为开口向上，顶点坐标为（-，），对称轴为直线x=-的抛物线，因为x∈[-1，1]，所以顶点能取到，则f（x）的最小值为
，根据抛物线图象可知x=1时，f（x）max=f（1）=7．
所以函数f（x）的值域为
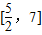
故答案为：
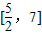
点评：本题主要考查学生会根据自变量的范围求二次函数所对应的值域，要求学生灵活运用二次函数的图象与性质求最值，属于基础题．
练习册系列答案
相关题目
函数f（x）=2x2-6x+1在区间[-1，1]上的最小值为（ ）
| A、9 | ||
| B、-3 | ||
C、
| ||
D、
|