题目内容
在△ABC中,角A,B,C的对边分别为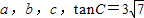 .
.(1)求cosC;
(2)若
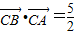 ,且a+b=9,求c.
,且a+b=9,求c.
【答案】分析:(1)由tanC的值,利用同角三角函数间的基本关系即可求出cosC的值;
(2)利用平面向量的数量积运算法则计算已知等式,将cosC值代入求出ab的值,将a+b=9两边平方,把ab的值代入求出a2+b2的值,再利用余弦定理即可求出c的值.
解答:解:(1)∵tanC=3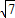 ,∴
,∴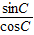 =3
=3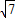 ,
,
又∵sin2C+cos2C=1,
解得:cosC=± ,
,
∵tanC>0,∴C是锐角,
∴cosC= ;
;
(2)∵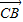 •
•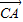 =abcosC=
=abcosC= ab=
ab= ,
,
∴ab=20,
又∵a+b=9,
∴两边平方得:a2+2ab+b2=81,
∴a2+b2=41,
∴由余弦定理得:c2=a2+b2-2abcosC=36,
∴c=6.
点评:此题考查了余弦定理,平面向量的数量积运算法则,以及同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.
(2)利用平面向量的数量积运算法则计算已知等式,将cosC值代入求出ab的值,将a+b=9两边平方,把ab的值代入求出a2+b2的值,再利用余弦定理即可求出c的值.
解答:解:(1)∵tanC=3
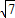 ,∴
,∴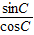 =3
=3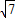 ,
,又∵sin2C+cos2C=1,
解得:cosC=±
 ,
,∵tanC>0,∴C是锐角,
∴cosC=
 ;
;(2)∵
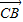 •
•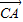 =abcosC=
=abcosC= ab=
ab= ,
,∴ab=20,
又∵a+b=9,
∴两边平方得:a2+2ab+b2=81,
∴a2+b2=41,
∴由余弦定理得:c2=a2+b2-2abcosC=36,
∴c=6.
点评:此题考查了余弦定理,平面向量的数量积运算法则,以及同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |