Question

【题目】已知函数f（x）＝x2+2﹣alnx﹣bx（a＞0）．

（Ⅰ）若a＝1，b＝3，求函数y＝f（x）在（1，f（1））处的切线方程；

（Ⅱ）若f（x1）＝f（x2）＝0，且x1≠x2，证明：f′（）＞0．

Answer 1

【答案】（Ⅰ）；（Ⅱ）见解析.

【解析】

（Ⅰ）求f（x）的导数，可得切线的斜率，以及切点，由点斜式方程可得切线方程；

（Ⅱ）由函数零点定义，两方程相减可得两个零点之间的关系，用变量集中的方法，把两个零点集中为一个变量，求导数，判断单调性，即可得证..

解：（Ⅰ）若a＝1，b＝3，f（x）＝x2+2﹣lnx﹣3x，

导数为f′（x）＝2x﹣﹣3，

可得在x＝1处切线的斜率为﹣2，

f（1）＝0，可得切线方程为y＝﹣2（x﹣1），

即为2x+y﹣2＝0；

（Ⅱ）证明：若f（x1）＝f（x2）＝0，且x1≠x2，

可得x12+2﹣alnx1﹣bx1＝0，x22+2﹣alnx2﹣bx2＝0，

两式相减可得（x1﹣x2）（x1+x2）﹣a（lnx1﹣lnx2）﹣b（x1﹣x2）＝0，

即有x1+x2﹣b＝a，

可设x0＝，

由f′（x0）＝2x0﹣﹣b＝（x1+x2﹣b）﹣

＝a﹣

＝[ln﹣]

＝[ln﹣]，

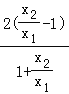令t＝，t＞1，可得f′（x0）＝[lnt﹣]，

设u（t）＝lnt﹣，t＞1，

导数为u′（t）＝﹣＝＞0，

可得u（t）在t＞1递增，且u（1）＝0，

可得u（t）＞u（1）＝0，

即lnt﹣＞0，

又a＞0，x2﹣x1＞0，可得f′（x0）＞0，

综上可得f′（）＞0．