题目内容
已知等比数列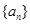 为递增数列,且
为递增数列,且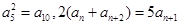 ,
,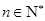 .
.
(Ⅰ)求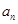 ;
;
(Ⅱ)令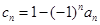 ,不等式
,不等式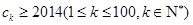 的解集为
的解集为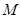 ,求所有
,求所有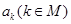 的和.
的和.
【答案】
(Ⅰ)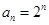 ;(Ⅱ)
;(Ⅱ)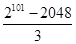 .
.
【解析】
试题分析:(Ⅰ)要求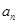 的通项公式,需要求出
的通项公式,需要求出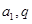 ,设
,设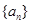 的首项为
的首项为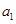 ,公比为
,公比为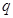 ,根据
,根据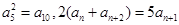 ,
,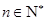 ,得
,得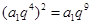 ,
,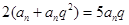 ,解得
,解得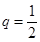 (舍)或
(舍)或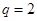 ,所以
,所以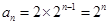 .(Ⅱ)将
.(Ⅱ)将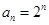 代入
代入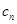 得,
得,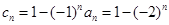 ,因为出现
,因为出现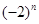 ,需要分奇偶项讨论. 当
,需要分奇偶项讨论. 当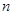 为偶数,
为偶数,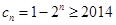 ,即
,即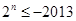 ,不成立,当
,不成立,当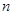 为奇数,
为奇数,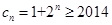 ,即
,即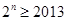 ,而
,而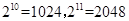 ,所以
,所以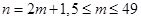 ,则
,则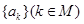 组成首项为
组成首项为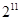 ,公比为
,公比为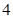 的等比数列,则所有
的等比数列,则所有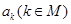 的和
的和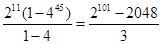 .
.
试题解析:(Ⅰ)设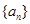 的首项为
的首项为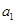 ,公比为
,公比为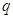 ,
,
所以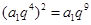 ,解得
,解得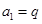
又因为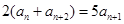 ,所以
,所以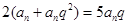
则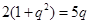 ,
,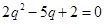 ,解得
,解得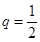 (舍)或
(舍)或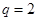
所以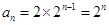
(Ⅱ)则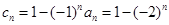 ,
,
当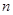 为偶数,
为偶数,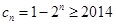 ,即
,即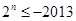 ,不成立
,不成立
当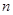 为奇数,
为奇数,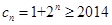 ,即
,即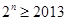 ,
,
因为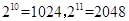 ,所以
,所以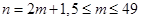
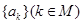 组成首项为
组成首项为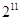 ,公比为
,公比为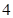 的等比数列
的等比数列
则所有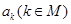 的和
的和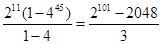 .
.
考点:1.等差、等比数列的性质;2.数列与不等式的简单应用.

练习册系列答案
相关题目
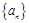 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数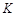 ,若任意的
,若任意的 ,
,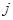 (
(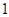 ≤
≤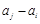 仍是
仍是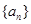 为“
为“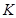 项可减数列”.
项可减数列”.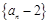 是“
是“ 项的和
项的和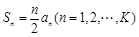 ;
;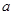 使得数列
使得数列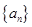 满足:若
满足:若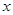 是数列
是数列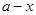 也是数列
也是数列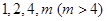 是“兑换系数”为
是“兑换系数”为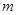 和
和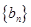 的项数是
的项数是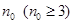 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列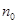 和
和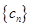 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.