题目内容
设全集U=R，A={x|x（x+3）＜0}，B={x|x＜-1}，则图中阴影部分表示的集合为（ ）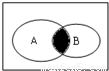
A．（-1，0）
B．（-3，-1）
C．[-1，0）
D．（-∞，-1）
【答案】分析：先解不等式求出A={x|-3＜x＜0}，再通过图象知道所求为A，B的公共部分，即取交集，结合集合B即可得到答案．
解答：解：因为x（x+3）＜0⇒-3＜x＜0
∴A={x|-3＜x＜0}，
由图得：所求为A，B的公共部分，即取交集．
∵B={x|x＜-1}，
∴A∩B={x|-3＜x＜-1}，
故选：B．
点评：本题主要考查不等式的解法以及Venn图表达集合的关系及运算．这一类型题目一般出现在前三题中，属于送分题．
解答：解：因为x（x+3）＜0⇒-3＜x＜0
∴A={x|-3＜x＜0}，
由图得：所求为A，B的公共部分，即取交集．
∵B={x|x＜-1}，
∴A∩B={x|-3＜x＜-1}，
故选：B．
点评：本题主要考查不等式的解法以及Venn图表达集合的关系及运算．这一类型题目一般出现在前三题中，属于送分题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
设全集U=R，A={x|ax+1=0}，B={1，2}，若A∩（?UB）=?，则实数a的取值集合是（ ）
| A、{0} | ||
| B、? | ||
C、{-1，-
| ||
D、{-1，-
|