题目内容
已知结论:“正三角形中心到顶点的距离是到对边中点距离的2倍”.若把该结论推广到空间,则有结论:
________.
正四面体的中心到顶点的距离是到对面中心距离的3倍
分析:这种类比的题目从平面上类比到空间中基本内容可以类比写出,只是这里要用的几倍要通过运算得到,因此画出图形,设出正四面体的棱长,在一系列等边三角形和直角三角形中,主要应用勾股定理,求出中心到底面中心的距离和到顶点的距离,得到比值.
解答: 解:设正四面体的棱长是1,中心O到底面中心F的距离是r,
解:设正四面体的棱长是1,中心O到底面中心F的距离是r,
在△BCD中,
BE= ,EF=
,EF= ,BF=
,BF= ,
,
OF=r,AO=BO= -r
-r
在直角三角形中, ,
,
∴r=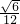 ,
,
∵AO= ,
,
∴
∴类比平面上的结论,得到:正四面体的中心到顶点的距离是到对面中心距离的三倍.
故答案为:正四面体的中心到顶点的距离是到对面中心距离的三倍.
点评:本题考查利用类比的方法写出从平面到空间的结论.这种类比解题时要注意若出现具体的数字,一定要通过运算得到准确的结果.
分析:这种类比的题目从平面上类比到空间中基本内容可以类比写出,只是这里要用的几倍要通过运算得到,因此画出图形,设出正四面体的棱长,在一系列等边三角形和直角三角形中,主要应用勾股定理,求出中心到底面中心的距离和到顶点的距离,得到比值.
解答:
 解:设正四面体的棱长是1,中心O到底面中心F的距离是r,
解:设正四面体的棱长是1,中心O到底面中心F的距离是r,在△BCD中,
BE=
 ,EF=
,EF= ,BF=
,BF= ,
,OF=r,AO=BO=
 -r
-r在直角三角形中,
 ,
,∴r=
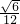 ,
,∵AO=
 ,
,∴

∴类比平面上的结论,得到:正四面体的中心到顶点的距离是到对面中心距离的三倍.
故答案为:正四面体的中心到顶点的距离是到对面中心距离的三倍.
点评:本题考查利用类比的方法写出从平面到空间的结论.这种类比解题时要注意若出现具体的数字,一定要通过运算得到准确的结果.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目