题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c(其中a≤b≤c),设向量 ,
, ,且向量
,且向量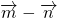 为单位向量.
为单位向量.
(1)求∠B的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.
解:(1)∵ ,向量
,向量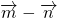 为单位向量--------------------(2分)
为单位向量--------------------(2分)
∴ --------------------(4分)
--------------------(4分)
∴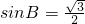
又B为三角形的内角,由a≤b≤c,故 --------------------(6分)
--------------------(6分)
(2)根据正弦定理,知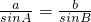 ,即
,即 ,
,
∴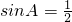 ,又a≤b≤c,∴
,又a≤b≤c,∴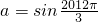 --------------------(9分)
--------------------(9分)
∵ ,∴C=
,∴C= ,
,
∴△ABC的面积= ----------------------(12分)
----------------------(12分)
分析:(1)根据向量 ,
, ,且向量
,且向量 为单位向量,可得
为单位向量,可得 ,由于B为三角形的内角,由a≤b≤c,故可得∠B的大小;
,由于B为三角形的内角,由a≤b≤c,故可得∠B的大小;
(2)根据正弦定理得 ,结合a≤b≤c,可得
,结合a≤b≤c,可得 ,从而C=
,从而C= ,故可求△ABC的面积.
,故可求△ABC的面积.
点评:本题以向量为载体,考查向量的数量积运算,考查正弦定理的运用,有一定的综合性.
 ,向量
,向量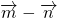 为单位向量--------------------(2分)
为单位向量--------------------(2分)∴
 --------------------(4分)
--------------------(4分)∴
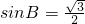
又B为三角形的内角,由a≤b≤c,故
 --------------------(6分)
--------------------(6分)(2)根据正弦定理,知
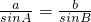 ,即
,即 ,
,∴
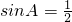 ,又a≤b≤c,∴
,又a≤b≤c,∴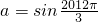 --------------------(9分)
--------------------(9分)∵
 ,∴C=
,∴C= ,
,∴△ABC的面积=
 ----------------------(12分)
----------------------(12分)分析:(1)根据向量
 ,
, ,且向量
,且向量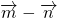 为单位向量,可得
为单位向量,可得 ,由于B为三角形的内角,由a≤b≤c,故可得∠B的大小;
,由于B为三角形的内角,由a≤b≤c,故可得∠B的大小;(2)根据正弦定理得
 ,结合a≤b≤c,可得
,结合a≤b≤c,可得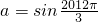 ,从而C=
,从而C= ,故可求△ABC的面积.
,故可求△ABC的面积.点评:本题以向量为载体,考查向量的数量积运算,考查正弦定理的运用,有一定的综合性.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |