题目内容
4、已知x1是方程x+lgx=3的根,x2是方程x+10x=3的根,则x1+x2值为
3
.分析:第一个方程:lgx=3-x.第二个方程,10x=3-x,lg(3-x)=x.注意第二个方程,如果做变量代换y=3-x,则lgy=3-y,其实是与第一个方程一样的.那么,如果x1,x2是两个方程的解,则必有x1=3-x2,也就是说,x1+x2=3.
解答:解:∵x+lgx=3,∴lgx=3-x.
∵x+10x=3,∴10x=3-x,
∴lg(3-x)=x.如果做变量代换y=3-x,则lgy=3-y,
∵x1是方程x+lgx=3的根,x2是方程x+10x=3的根,
∴x1=3-x2,∴x1+x2=3.
答案:3.
∵x+10x=3,∴10x=3-x,
∴lg(3-x)=x.如果做变量代换y=3-x,则lgy=3-y,
∵x1是方程x+lgx=3的根,x2是方程x+10x=3的根,
∴x1=3-x2,∴x1+x2=3.
答案:3.
点评:本题考查对数函数的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 时,f(x)取得极小值
时,f(x)取得极小值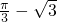 .
.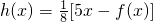 ,设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由.
,设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由. =1上的动点,以M为切点的切线l与直线y=2相交于点P.
=1上的动点,以M为切点的切线l与直线y=2相交于点P. ,则以Q为切点的椭圆的切线方程是:
,则以Q为切点的椭圆的切线方程是: .
.