题目内容
M、N、P分别是正方体ABCD—A1B1C1D1中棱CC1、BC、CD的中点，求证：A1P⊥面DMN.
解析：
建立上图所示的空间直角坐标系.
设正方体棱长为2,则D（0，0，0），A1（2，0，2），P（0，1，0），M（0，2，1），N（1，2，0），∴向量
=（-2，1，-2），
=（0，2，1），
=（1，2，0）.
∴
·
=0，
·
=0.
∴
⊥
，
⊥
.
故A1P⊥面DMN.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
分别是x、y轴正方向的单位向量，点P（x，y）为曲线C上任意一点，
且满足
．
平分？若存在求出l的倾斜角α的范围，若不存在说明理由．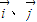
分别是x、y轴正方向的单位向量，点P（x，y）为曲线C上任意一点，
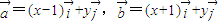且满足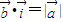
．
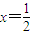平分？若存在求出l的倾斜角α的范围，若不存在说明理由．