题目内容
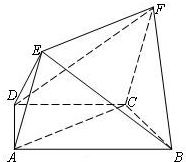 如图,多面体EF-ABCD中,ABCD是梯形,AB∥CD,ACFE是矩形,面ACFE⊥面ABCD,AD=DC=CB=AE=a,∠ACB=
如图,多面体EF-ABCD中,ABCD是梯形,AB∥CD,ACFE是矩形,面ACFE⊥面ABCD,AD=DC=CB=AE=a,∠ACB=| π | 2 |
(1)若M是棱EF上一点,AM∥平面BDF,求EM;
(2)求二面角B-EF-D的平面角的余弦值.
分析:(1)连接BD,记AC∩BD=O,在梯形ABCD中,由题意得∠ACD=∠CAB=∠DAC,由角之间的关系可得∠DAC=
,从而∠CBO=
,又∠ACB=
,CB=a,所以CO=
a,由AM∥平面BDF得AM∥FO.
(2)建立空间直角坐标系,利用向量的运算求出平面DEF的一个法向量为
=(0.2.-1),平面BEF的一个法向量为
=(0.1.1),进而由两个法向量求出二面角余弦值的大小.
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| ||
| 3 |
(2)建立空间直角坐标系,利用向量的运算求出平面DEF的一个法向量为
| n1 |
| n2 |
解答:解(1)连接BD,记AC∩BD=O,在梯形ABCD中,
因为AD=DC=CB=a,AB∥CD,
所以∠ACD=∠CAB=∠DAC,
π=∠ABC+∠BCD=∠DAB+∠ACD+ACB=3∠DAC+
,∠DAC=
,从而∠CBO=
,
又因为∠ACB=
,CB=a,所以CO=
a,
连接FO,由AM∥平面BDF得AM∥FO,
因为ACFE是矩形,所以EM=CO=
.
(2)以C为原点,CA、CB、CF分别为x轴、y轴、z轴建立空间直角坐标系,
则C(0,0,0),A(
a,0,0),B(0,a,0),D(
a,-
,0),F(0,0,a),E(
a,0,a),
设平面DEF的一个法向量为
=(r.s.t),
则有
,即
,
解得
=(0.2.-1),
同理可得平面BEF的一个法向量为
=(0.1.1),
观察知二面角B-EF-D的平面角为锐角,所以其余弦值为cosθ=
=
.
因为AD=DC=CB=a,AB∥CD,
所以∠ACD=∠CAB=∠DAC,
π=∠ABC+∠BCD=∠DAB+∠ACD+ACB=3∠DAC+
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
又因为∠ACB=
| π |
| 2 |
| ||
| 3 |
连接FO,由AM∥平面BDF得AM∥FO,
因为ACFE是矩形,所以EM=CO=
| ||
| 3 |
(2)以C为原点,CA、CB、CF分别为x轴、y轴、z轴建立空间直角坐标系,
则C(0,0,0),A(
| 3 |
| ||
| 2 |
| a |
| 2 |
| 3 |
设平面DEF的一个法向量为
| n1 |
则有
|
|
解得
| n1 |
同理可得平面BEF的一个法向量为
| n2 |
观察知二面角B-EF-D的平面角为锐角,所以其余弦值为cosθ=
|
| ||||
|
|
| ||
| 10 |
点评:解决此类问题的关键是熟悉几何体的结构特征,进而便于几何体的线面关系以及建立坐标系利用向量解决空间角与空间距离的问题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.
 .
.
 .
.
 .
.