题目内容
如图12,在△ABC中,∠B= ,AB=8,点D在BC边上,且CD=2,cos∠ADC=
,AB=8,点D在BC边上,且CD=2,cos∠ADC=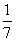 .
.
(1)求sin∠BAD;
(2)求BD,AC的长.
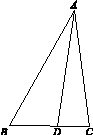
图12
解:(1) 在△ADC中,因为cos ∠ADC=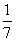 ,所以sin ∠ADC=
,所以sin ∠ADC= .
.
所以sin ∠BAD=sin(∠ADC-∠B)=sin ∠ADCcos B-cos ∠ADCsin B= ×
×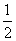 -
-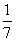 ×
× =
= .
.
(2)在△ABD中,由正弦定理得
BD= =
=
在△ABC中,由余弦定理得
AC2=AB2+BC2-2AB·BC·cos B
=82+52-2×8×5×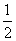 =49,
=49,
所以AC=7.

练习册系列答案
相关题目
 ;条件
;条件 ,若
,若 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
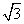 cos
cos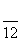 t-sin
t-sin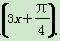
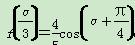 cos 2α,求cos α-sin α的值.
cos 2α,求cos α-sin α的值. (1)求实验室这一天的最大温差.
(1)求实验室这一天的最大温差.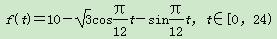 (1)求实验室这一天的最大温差.
(1)求实验室这一天的最大温差. .
. 时,求
时,求 的最值;
的最值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数.
上是单调函数. 的不等式
的不等式 (
( )
)