Question

各项均为正数的等比数列{a_n}满足a₁a₇=4，a₆=8，若函数的导数为f′（x），则=　　．

Answer 1

考点：

导数的运算；数列与函数的综合．

专题：

等差数列与等比数列．

分析：

利用等比数列和等差数列的通项公式、导数的运算法则即可得出．

解答：

解：由各项均为正数的等比数列{a_n}满足a₁a₇=4，a₆=8，设公比为q＞0，于是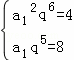，解得，

∴．

∴f^′（x）=…+，

∵=n×2^n﹣3×2^1﹣n=，

∴===．

故答案为．

点评：

熟练掌握等比数列和等差数列的通项公式、导数的运算法则是解题的关键．