题目内容
(12分) 设函数 (
(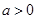 ),
), .
.
(1) 将函数 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数 的图象,试写出
的图象,试写出 的解析式及值域;
的解析式及值域;
(2) 关于 的不等式
的不等式 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数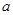 的取值范围;
的取值范围;
(3) 对于函数 与
与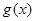 定义域上的任意实数
定义域上的任意实数 ,若存在常数
,若存在常数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数 与
与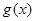 的“分界线”.设
的“分界线”.设 ,
, ,试探究
,试探究 与
与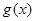 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
【答案】
(1) ,值域为
,值域为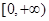
(2)解法一:不等式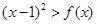 的解集中的整数恰有3个,
的解集中的整数恰有3个,
等价于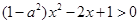 恰有三个整数解,故
恰有三个整数解,故 ,
,
令 ,由
,由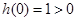 且
且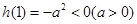 ,
,
所以函数 的一个零点在区间
的一个零点在区间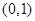 ,
,
则另一个零点一定在区间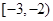 ,
,
故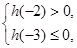 解之得
解之得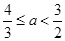 .
.
解法二: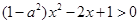 恰有三个整数解,故
恰有三个整数解,故 ,即
,即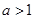 ,
,
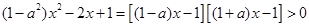 ,
,
所以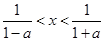 ,又因为
,又因为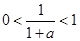 ,
,
所以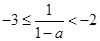 ,解之得
,解之得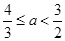 .
.
(3)设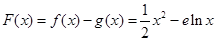 ,则
,则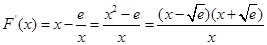 .
.
所以当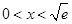 时,
时,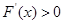 ;当
;当 时,
时,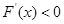 .
.
因此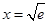 时,
时,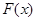 取得最小值
取得最小值 ,
,
则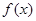 与
与 的图象在
的图象在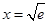 处有公共点
处有公共点 .
.
设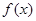 与
与 存在 “分界线”,方程为
存在 “分界线”,方程为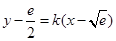 ,
,
即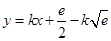 ,
,
由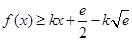 在
在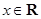 恒成立,则
恒成立,则 在
在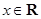 恒成立 .
恒成立 .
所以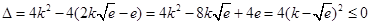 成立,
成立,
因此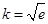 .
.
下面证明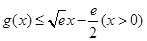 恒成立.
恒成立.
设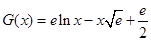 ,则
,则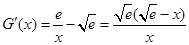 .
.
所以当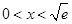 时,
时,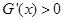 ;当
;当 时,
时,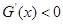 .
.
因此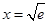 时
时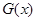 取得最大值
取得最大值 ,则
,则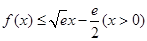 成立.
成立.
故所求“分界线”方程为: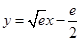 .
.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数y=
的定义域为M,值域为N,那么( )
| 1 | ||
1+
|
| A、M={x|x≠0},N={y|y≠0} |
| B、M={x|x≠0},N={y|y∈R} |
| C、M={x|x<0且x≠-1,或x>0},N={y|y<0或0<y<1或y>1} |
| D、M={x|x<-1或-1<x<0或x>0},N={y|y≠0} |