题目内容
已知O是坐标原点，经过P（3，2）且与OP垂直的直线方程是
3x+2y-13=0
3x+2y-13=0
．分析：先求出直线OP的斜率，再根据垂直关系得到所求直线的斜率，最后结合直线过P（3，2）即可求出结论．
解答：解：∵kOP=
，
∴所求直线的斜率为：k=-
，
∴所求直线方程：y-2=-
（x-3）⇒3x+2y-13=0．
故答案为：3x+2y-13=0．
| 2 |
| 3 |
∴所求直线的斜率为：k=-
| 3 |
| 2 |
∴所求直线方程：y-2=-
| 3 |
| 2 |
故答案为：3x+2y-13=0．
点评：本题主要考查直线的一般式方程与直线的垂直关系．解决本题的关键在于知道两直线垂直时，要么斜率相乘等于-1，要么一条直线斜率不存在，另一条斜率为0．
练习册系列答案
相关题目
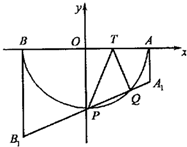已知T是半圆O的直径AB上一点，AB=2，OT=t（0＜t＜1）．以AB为腰的直角梯形AA1B1B中，AA1垂直于AT，且|AA1|=|AT|，BB1垂直于BT，且|BB1|=|BT|，A1B1交半圆于P，Q两点，建立如图所示直角坐标系，O为坐标原点．
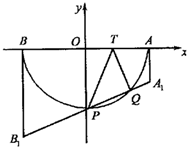已知T是半圆O的直径AB上一点，AB=2，OT=t（0＜t＜1）．以AB为腰的直角梯形AA1B1B中，AA1垂直于AT，且|AA1|=|AT|，BB1垂直于BT，且|BB1|=|BT|，A1B1交半圆于P，Q两点，建立如图所示直角坐标系，O为坐标原点．