题目内容
在北纬45°圈上的甲、乙两地,甲在东经30°,乙在西经60°处,若地球半径为R,则甲、乙两地的球面距离是 .
分析:由纬度的概念算出甲、乙两地所在的纬圆半径r=
R,根据经度差为90°得到两地的直线距离AB=R,可得点A、B与球心O构成等边三角形,所以球心角为60度,再利用球面距离公式即可算出甲、乙两地的球面距离.
| ||
| 2 |
解答:解:地球表面上,甲地的位置:北纬45°,东经30度;乙地的位置:北纬45°,西经60度.
设甲、乙两地对应球面上的A、B两点,地球的球心为O,如图所示.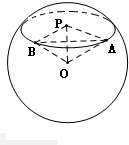
∵A、B两点在北纬45°圈上,∴A、B所在的纬圆半径r=R•cos45°=
R,
设北纬45度圈的圆心是P,
由甲、乙两地经度差是30°+60°=90°,可得∠APB=90°.
∴Rt△APB中,PA=PB=
R,AB=
=R.
因此△AOB中,OA=OB=AB=R,可得△AOB是边长为R的正三角形,
∴球心角为θ=∠AOB=
,可得甲、乙两地的球面距离为L=θR=
.
故答案为:
设甲、乙两地对应球面上的A、B两点,地球的球心为O,如图所示.

∵A、B两点在北纬45°圈上,∴A、B所在的纬圆半径r=R•cos45°=
| ||
| 2 |
设北纬45度圈的圆心是P,
由甲、乙两地经度差是30°+60°=90°,可得∠APB=90°.
∴Rt△APB中,PA=PB=
| ||
| 2 |
| PA2+PB2 |
因此△AOB中,OA=OB=AB=R,可得△AOB是边长为R的正三角形,
∴球心角为θ=∠AOB=
| π |
| 3 |
| πR |
| 3 |
故答案为:
| πR |
| 3 |
点评:本题给出北纬45°圈上的甲、乙两地的经度之差,求它们的球面距离.着重考查了经度、纬度的概念与球面距离的计算等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目