题目内容
（2013•南京二模）在△ABC中，已知角A，B，C所对的边分别为a，b，c，且
=
，
（1）求B；
（2）若tan(A+
)=7，求cosC的值．
| cosC |
| cosB |
| 2a-c |
| b |
（1）求B；
（2）若tan(A+
| π |
| 4 |
分析：（1）利用正弦定理、两角和的正弦公式、诱导公式、特殊角的三角函数值即可得出；
（2）利用两角和的正切公式平方关系、诱导公式、两角和的余弦公式即可得出．
（2）利用两角和的正切公式平方关系、诱导公式、两角和的余弦公式即可得出．
解答：解：（1）由正弦定理得
=
=
，
∴
=
，
∴
=
，化为sinBcosC+sinCcosB=2sinAcosB，
∴sin（B+C）=2sinAcosB，
∵B+C=π-A，∴sinA=2sinAcosB，
∵A∈（0，π），∴sinA≠0，得到cosB=
．
又B∈（0，π），∴B=
．
（2）∵tan(A+
)=7，∴
=7，解得tanA=
．
∵A∈（0，π）∴A为锐角．
∴cosA=
，sinA=
．
∴cosC=cos（π-A-B）=cos（A+B）=cos(A+
)=-cosAcos
+sinAsin
=-
×
+
×
=
．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴
| 2a-c |
| b |
| 2sinA-sinC |
| sinB |
∴
| cosC |
| cosB |
| 2sinA-sinC |
| sinB |
∴sin（B+C）=2sinAcosB，
∵B+C=π-A，∴sinA=2sinAcosB，
∵A∈（0，π），∴sinA≠0，得到cosB=
| 1 |
| 2 |
又B∈（0，π），∴B=
| π |
| 3 |
（2）∵tan(A+
| π |
| 4 |
| tanA+1 |
| 1-tanA |
| 3 |
| 4 |
∵A∈（0，π）∴A为锐角．
∴cosA=
| 4 |
| 5 |
| 3 |
| 5 |
∴cosC=cos（π-A-B）=cos（A+B）=cos(A+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 3 |
-4+3
| ||
| 10 |
点评：熟练掌握正弦定理、两角和的正弦余弦正切公式、诱导公式、特殊角的三角函数值是解题的关键．
练习册系列答案
相关题目
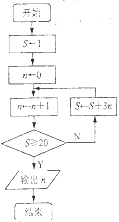（2013•南京二模）如图是一个算法流程图，其输出的n的值是