题目内容
设函数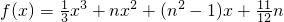 的导函数在区间[n,+∞)上的最小值为an(n∈N*)
的导函数在区间[n,+∞)上的最小值为an(n∈N*)
(1)求an;
(2)设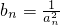 ,求数列bn]的前n项的和Sn.
,求数列bn]的前n项的和Sn.
解:(1)由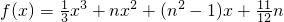
得f'(x)=x2+2nx+(n2-1)
在区间[n,+∞)上的最小值为 ,
,
∴an= .
.
(2)因为bn= ,
,
∴Sn=b1+b2+b3+…+bn
=
=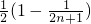 .
.
分析:(1)由题设得f'(x)=x2+2nx+(n2-1),在区间[n,+∞)上的最小值为 ,由此可求出an;
,由此可求出an;
(2)因为bn= ,所以
,所以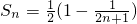 .
.
点评:本题考查数列的性质和应用,解题时要结合实际情况和数列的性质耐心寻找突破口,准确地进行求解.
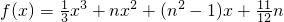
得f'(x)=x2+2nx+(n2-1)
在区间[n,+∞)上的最小值为
 ,
,∴an=
 .
.(2)因为bn=
 ,
,∴Sn=b1+b2+b3+…+bn
=

=
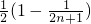 .
.分析:(1)由题设得f'(x)=x2+2nx+(n2-1),在区间[n,+∞)上的最小值为
 ,由此可求出an;
,由此可求出an;(2)因为bn=
 ,所以
,所以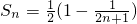 .
.点评:本题考查数列的性质和应用,解题时要结合实际情况和数列的性质耐心寻找突破口,准确地进行求解.

练习册系列答案
相关题目
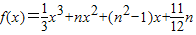 的导函数在区间[n,+∞)上的最小值为an(n∈N*)
的导函数在区间[n,+∞)上的最小值为an(n∈N*)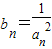 ,求数列bn]的前n项的和Sn.
,求数列bn]的前n项的和Sn.