题目内容
已知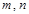
为两条不同直线,
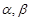为两个不同平面,给出下列命题:
①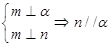
②
③
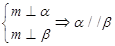④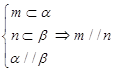
其中的正确命题序号（ ）
| A．③④ | B．②③ |
| C．①② | D．①②③④ |
B
解析试题分析：①不正确，因为还有可能
； ②③均正确，线面垂直的性质定理；④不正确，因为两直线还有可能异面。
考点：1线线位置关系、线面位置关系；2线线垂直、线面垂直；3线线平行、线面平行。
练习册系列答案
阅读快车系列答案
相关题目
空间四边形ABCD中，AD=BC=2,E,F分别是AB,CD的中点，EF＝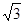 
，则异面直线AD,BC所成的角为( )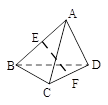
| A．30° | B．60° | C．90° | D．120° |
正方体ABCD－A1B1C1D1中，若E是线段A1C1上一动点，那么直线CE恒垂直于
| A．AC | B．BD | C．A1D | D．A1D1 |
三棱锥
中，
分别是
的中点，则四边形
是（ ）
| A．菱形 | B．矩形 | C．梯形 | D．正方形 |
四棱锥P-ABCD中,底面ABCD是平行四边形,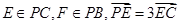
,
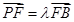,若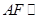
平面BDE,则
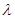的值为 ( )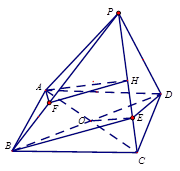
| A．1 | B．3 | C．2 | D．4 |
对于直线m,n和平面α,β,α⊥β的一个充分条件是( )
| A．m⊥n,m∥α,n∥β | B．m⊥n,α∩β=m,n?α |
| C．m∥n,n⊥β,m?α | D．m∥n,m⊥α,n⊥β |
如图，在正方体ABCDA1B1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有 ( )．
| A．3个 | B．4个 |
| C．5个 | D．6个 |
已知m和n是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m⊥β的是( )．
| A．α⊥β，且m?α | B．m∥n，且n⊥β |
| C．α⊥β，且m∥α | D．m⊥n，且n∥β |
已知α，β是两个不同的平面，m，n是两条不重合的直线，下列命题中正确的是( )．
| A．若m∥α，α∩β＝n，则m∥n |
| B．若m⊥α，m⊥n，则n∥α |
| C．若m⊥α，n⊥β，α⊥β，则m⊥n |
| D．若α⊥β，α∩β＝n，m⊥n，则m⊥β |