题目内容
不等式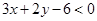
表示的平面区域是 （ ）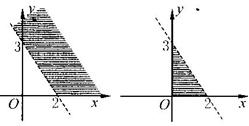
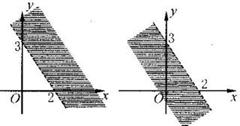
A. B. C. D.
D
解析试题分析：根据已知的不等式可知，原点的坐标满足不等式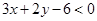，那么说明区域中含有原点，排除旋下那个A,C,同时要注意到直线的一侧的部分包括整个半平面，因此B错误，只有选D.
考点：本试题考查了不等式表示的平面区域知识点。
点评：确定平面区域的方法，就是运用特殊点法代入判定，而特殊点一般式选择原点，或者是原点附近的点，同时要注意虚实要分，属于基础题。
练习册系列答案
相关题目
已知实数
满足条件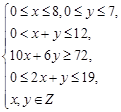
则使得目标函数
取得最大值的的值分别为( )
| A．0，12 | B．12，0 | C．8，4 | D．7，5 |
若实数
满足：
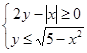，则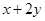
的最大值是（ ）
| A．3 | B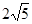． | C．5 | D． |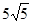
若
满足约束条件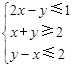
，目标函数
仅在点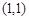
处取得小值，则k的取值范围为
| A．（－1，2） | B．（－4，2） | C．(－4，0] | D．（－2，4） |
点
满足平面区域：
，点
满足：
，则
的最小值是( )
A． | B． | C． | D． |
若关于
的不等式组
表示的区域为三角形，则实数
的取值范围是( )
A． | B． | C． | D． |
设平面区域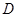
是由直线
和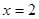
所围成的三角形（含边界与内部）．若点
，则目标函数
的最大值为（ ）
A． | B． | C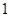． | D． |
设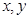
满足约束条件
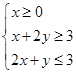,则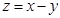
的最大值是（ ）
A． | B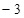． | C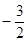． | D．0 |
若实数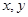
满足不等式组
（
为常数），且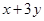
的最大值为12，
则实数=（ ）
| A．0 | B． | C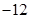． | D．任意实数 |