题目内容
若函数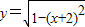 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为此数列公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为此数列公比的数是( )A.

B.

C.
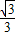
D.
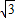
【答案】分析:根据平面几何切割线定理:从圆外一点做圆的切线和割线,则切线长是割线与它的圆外部分的比例中项.假设存在,则可计算出公比的范围,从而可下结论.
解答:解:根据平面几何切割线定理:从圆外一点做圆的切线和割线,则切线长是割线与它的圆外部分的比例中项.
鉴于此,从原点作该半圆的切线,切线长为: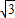
设割线与半圆的另外两个交点到原点的距离分别是a和b,则b=aq2,且ab=(aq)2=3,所以aq=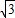
所以q=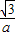
当1≤a≤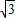 ,则1≤q≤
,则1≤q≤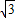 ;
;
当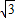 ≤a≤3时,
≤a≤3时,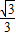 ≤q≤1
≤q≤1
考查四个选项,只有A选项不符合上述范围
故选A.
点评:本题的考点是等比关系的确定,主要课程等比数列的定义,等比中项及切割线定理,属于基础题.
解答:解:根据平面几何切割线定理:从圆外一点做圆的切线和割线,则切线长是割线与它的圆外部分的比例中项.
鉴于此,从原点作该半圆的切线,切线长为:
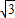
设割线与半圆的另外两个交点到原点的距离分别是a和b,则b=aq2,且ab=(aq)2=3,所以aq=
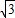
所以q=
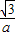
当1≤a≤
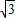 ,则1≤q≤
,则1≤q≤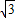 ;
;当
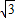 ≤a≤3时,
≤a≤3时,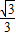 ≤q≤1
≤q≤1考查四个选项,只有A选项不符合上述范围
故选A.
点评:本题的考点是等比关系的确定,主要课程等比数列的定义,等比中项及切割线定理,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 .
.  时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 的取值范围;
的取值范围; 两点的横坐标是函数
两点的横坐标是函数 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.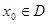 ,使
,使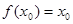 成立,则称以
成立,则称以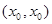 为坐标的点为函数
为坐标的点为函数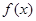 图象上的不动点。
图象上的不动点。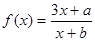 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求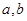 应满足的条件;
应满足的条件;