题目内容
(本小题满分12分)四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.
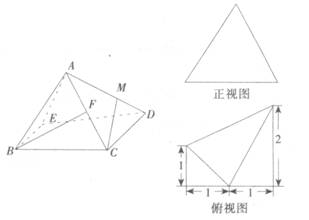
(I)若F为AC的中点,当点M在棱AD上移动时,是否总有BF丄CM,请说明理由.
(II)求三棱锥C_ADE的高.
【答案】
(Ⅰ)总有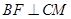 理由如下:
理由如下:
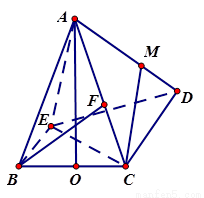
取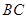 的中点
的中点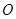 ,连接
,连接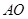 ,
,
由俯视图可知,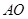
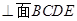 ,
,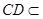
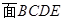 ,
,
所以 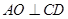 ……………………2分
……………………2分
又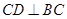 ,所以
,所以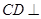 面
面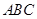 ,
,
故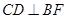 .
.
因为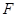 是
是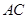 的中点,所以
的中点,所以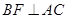 .…………………4分
.…………………4分
又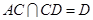 故
故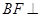 面
面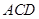 ,
,
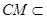 面
面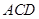 ,所以
,所以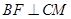 . ……………………6分
. ……………………6分
(Ⅱ)由(Ⅰ)可知,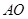
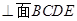 ,
,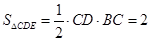 ,
,
又在正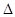 ABC中,
ABC中, ,
,
所以 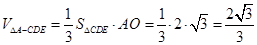 , ……………………8分
, ……………………8分
在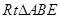 中,
中,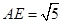 ,
,
在直角梯形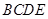 中,
中,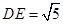 ,
,
在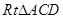 中,
中,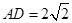 ,
,
在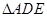 中,可求
中,可求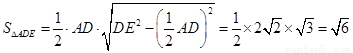 , ………10分
, ………10分
设三棱锥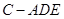 的高为
的高为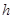 ,
,
则 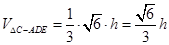 ,
,
又 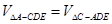 ,
,
可得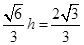 ,解得
,解得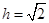 .
.
所以,三棱锥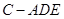 的高为
的高为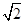 .
……………………12分
.
……………………12分
【解析】(1)根据俯视图可确定平面ABC与底面BECD垂直,并且点A在底面上的射影在BC的中点位置。还可以得到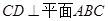 ,所以
,所以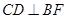 ,又BF丄AC,所以可证出
,又BF丄AC,所以可证出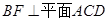 ,进而证明出BF丄CM恒成立。 (2)利用体积法,易求三棱锥A_CDE的体积,然后再求出三角形ADE的面积,根据体积相等即可求三棱锥C_ADE的高。
,进而证明出BF丄CM恒成立。 (2)利用体积法,易求三棱锥A_CDE的体积,然后再求出三角形ADE的面积,根据体积相等即可求三棱锥C_ADE的高。

练习册系列答案
相关题目