题目内容
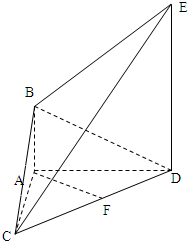 (2012•宿州三模)如图,AB⊥平面ACD,DE⊥平面ACD,AD=AC=AB=
(2012•宿州三模)如图,AB⊥平面ACD,DE⊥平面ACD,AD=AC=AB=| 1 | 2 |
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE.
分析:(Ⅰ)取CE的中点M,连接MF,MB,在△CDE中,MF∥DE,MF=
DE,又因为AB⊥面ACD,DE⊥面ACD.所以AB∥DE,且AB=
DE,由此能够证明AF∥平面BCE.
(Ⅱ)AC=AD,F是CD中点,所以AF⊥CD,又DE⊥面ACD,所以DE⊥AF,CD∩DE=D,AF⊥平面CDE,由此能够证明平面BCE⊥平面CDE.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)AC=AD,F是CD中点,所以AF⊥CD,又DE⊥面ACD,所以DE⊥AF,CD∩DE=D,AF⊥平面CDE,由此能够证明平面BCE⊥平面CDE.
解答: 解:(Ⅰ)取CE的中点M,连接MF,MB,
解:(Ⅰ)取CE的中点M,连接MF,MB,
在△CDE中,MF∥DE,MF=
DE,
又因为AB⊥面ACD,DE⊥面ACD.
所以AB∥DE,且AB=
DE,
∴MF∥AB,且MF=AB,
∴四边形ABMF是平行四边形,
AF∥BM,AF?面BCE,所以BM?面BCE,
故AF∥平面BCE.…(6分)
(Ⅱ)AC=AD,F是CD中点,所以AF⊥CD,
又DE⊥面ACD,所以DE⊥AF,CD∩DE=D,
AF⊥平面CDE,
由(Ⅰ)知AF∥BM,BM⊥平面CDE,
BM?面BCE,
故平面BCE⊥平面CDE.…(12分)
 解:(Ⅰ)取CE的中点M,连接MF,MB,
解:(Ⅰ)取CE的中点M,连接MF,MB,在△CDE中,MF∥DE,MF=
| 1 |
| 2 |
又因为AB⊥面ACD,DE⊥面ACD.
所以AB∥DE,且AB=
| 1 |
| 2 |
∴MF∥AB,且MF=AB,
∴四边形ABMF是平行四边形,
AF∥BM,AF?面BCE,所以BM?面BCE,
故AF∥平面BCE.…(6分)
(Ⅱ)AC=AD,F是CD中点,所以AF⊥CD,
又DE⊥面ACD,所以DE⊥AF,CD∩DE=D,
AF⊥平面CDE,
由(Ⅰ)知AF∥BM,BM⊥平面CDE,
BM?面BCE,
故平面BCE⊥平面CDE.…(12分)
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•宿州三模)程序框图如图所示,该程序运行后输出的S的值是( )
(2012•宿州三模)程序框图如图所示,该程序运行后输出的S的值是( )