题目内容
已知(x+2)4=a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4=
65
65
.分析:由题设条件知,此是一个二项式系数有关的问题,可令x=1,求出所有项的系数和,由于a0=24=16,从所有项的系数和中减去16即可得到a1+a2+a3+a4的值
解答:解:由题意,令x=1,得a4+a3+a2+a1+a0=34=81
由二项式的系数知a0=24=16
故a1+a2+a3+a4=81-16=65
故答案为65
由二项式的系数知a0=24=16
故a1+a2+a3+a4=81-16=65
故答案为65
点评:本题考察二项式系数的性质,求解的关键是掌握二项式系数的公式及所有项系数和的求法,本题有一易混点,即区分开二项式系数与项的系数的不同,二项式的系数指的是Cnk,项的系数指的是二项式系数与项中常数的乘积

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,x∈[2,4]
,x∈[2,4]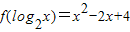 ,x∈[2,4]
,x∈[2,4]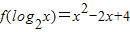 ,x∈[2,4]
,x∈[2,4]