题目内容
如图,为处理含有某种杂质的污水,要制造一个底宽为2 m的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a m,高度为b m,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60 m2,问当a、b各为多少时,沉淀后流出的水中该杂质的质量分数最小(A,B孔的面积忽略不计).
解法一:设流出的水中杂质的质量分数为y,由题意y=![]() (k>0),其中k为比例系数.
(k>0),其中k为比例系数.
又据题设2×2b+2ab+2a=60(a>0,b>0),
∴b=![]() (由a>0,b>0,可得a<30),
(由a>0,b>0,可得a<30),
∴y=![]() =
= .令t=a+2,则a=t-2,
.令t=a+2,则a=t-2,
从而![]() =
=![]() =
=![]()
=34-(t+![]() )≤34-2
)≤34-2![]() =18,
=18,
∴y=![]()
当且仅当t=![]() ,即t=8时取等号,
,即t=8时取等号,
∴a=6时取“=”.由a=6可得b=3.
综上所述,当a=6 m,b=3 m时,经沉淀后流出的水中杂质的质量分数最小.
解法二:设流出的水中杂质的质量分数为y,依题意y=![]() ,其中k为比例系数,k>0,要求y的最小值,必须求解ab的最大值.
,其中k为比例系数,k>0,要求y的最小值,必须求解ab的最大值.
题设4b+2ab+2a=60,即ab+2b+a=30(a>0,b>0),∵a+2b≥2![]() (当且仅当a=2b时取“=”),∴ab+2
(当且仅当a=2b时取“=”),∴ab+2![]()
![]() ≤30,可解得0<ab≤18.
≤30,可解得0<ab≤18.
由a=2b,及ab+a+2b=30,可得a=6,b=3.
即a=6,b=3时,ab取最大值,从而y值最小.
温馨提示
形如y=![]() 的分式函数,求最值时常常等价转化为函数y=
的分式函数,求最值时常常等价转化为函数y=![]() +bx(a>0,b>0,x>0),再求最值.等价转化的步骤为:
+bx(a>0,b>0,x>0),再求最值.等价转化的步骤为:
(1)变量替换,目的是使分母变单项式,易分离系数.
(2)分离系数,化归成可用均值不等式求最值的问题.
(3)变量换成z,注意z>0.
(4)若满足“一正、二定、三相等”,用均值不等式求解.
若不满足“一正、二定、三相等”,用函数y=![]() +bx的单调性求解.
+bx的单调性求解.
此类题常见的错误是直接套用均值不等式,忽视等号取不到这一点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
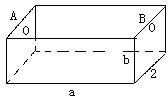 如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).
如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).

