题目内容
设 的展开式的各项系数绝对值之和为M,二项式系数之和为N,若M-N=240,则展开式中x的有理项的项数为
的展开式的各项系数绝对值之和为M,二项式系数之和为N,若M-N=240,则展开式中x的有理项的项数为
- A.1
- B.2
- C.3
- D.4
C
分析:根据二项式定理,可得 的展开式的通项为Tr+1=(-1)rCnr•3n-r•
的展开式的通项为Tr+1=(-1)rCnr•3n-r• ,即可得各项系数的绝对值,进而可得M=Cn0•3n+Cn1•3n-1+Cn2•3n-2+…+Cnn•30=(3+1)r=4n,又由题意,可得4n-2n=240,解可得n的值,可得其展开式的通项公式,分析x的指数可得答案.
,即可得各项系数的绝对值,进而可得M=Cn0•3n+Cn1•3n-1+Cn2•3n-2+…+Cnn•30=(3+1)r=4n,又由题意,可得4n-2n=240,解可得n的值,可得其展开式的通项公式,分析x的指数可得答案.
解答:根据题意, 的展开式的通项为Tr+1=Cnr•(3x)n-r•(-
的展开式的通项为Tr+1=Cnr•(3x)n-r•(- )r=(-1)rCnr•3n-r•
)r=(-1)rCnr•3n-r• ;
;
则第r+1项系数的绝对值为|Tr+1|=Cnr•3n-r,
M=Cn0•3n+Cn1•3n-1+Cn2•3n-2+…+Cnn•30=(3+1)r=4n,
其展开式的二项式系数之和为N=2n,
又由M-N=240,可得4n-2n=240,
解可得2n=16,则n=4;
则 的展开式的通项为Tr+1=(-1)rC4r•34-r•
的展开式的通项为Tr+1=(-1)rC4r•34-r• ;
;
分析可得,r=0、2、4时,Tr+1为有理项,
则展开式中x的有理项的项数为3;
故选C.
点评:本题考查二项式定理的应用,难点在于得到各项系数绝对值的表达式,进而由二项式定理求出M的值.
分析:根据二项式定理,可得
 的展开式的通项为Tr+1=(-1)rCnr•3n-r•
的展开式的通项为Tr+1=(-1)rCnr•3n-r• ,即可得各项系数的绝对值,进而可得M=Cn0•3n+Cn1•3n-1+Cn2•3n-2+…+Cnn•30=(3+1)r=4n,又由题意,可得4n-2n=240,解可得n的值,可得其展开式的通项公式,分析x的指数可得答案.
,即可得各项系数的绝对值,进而可得M=Cn0•3n+Cn1•3n-1+Cn2•3n-2+…+Cnn•30=(3+1)r=4n,又由题意,可得4n-2n=240,解可得n的值,可得其展开式的通项公式,分析x的指数可得答案.解答:根据题意,
 的展开式的通项为Tr+1=Cnr•(3x)n-r•(-
的展开式的通项为Tr+1=Cnr•(3x)n-r•(- )r=(-1)rCnr•3n-r•
)r=(-1)rCnr•3n-r• ;
;则第r+1项系数的绝对值为|Tr+1|=Cnr•3n-r,
M=Cn0•3n+Cn1•3n-1+Cn2•3n-2+…+Cnn•30=(3+1)r=4n,
其展开式的二项式系数之和为N=2n,
又由M-N=240,可得4n-2n=240,
解可得2n=16,则n=4;
则
 的展开式的通项为Tr+1=(-1)rC4r•34-r•
的展开式的通项为Tr+1=(-1)rC4r•34-r• ;
;分析可得,r=0、2、4时,Tr+1为有理项,
则展开式中x的有理项的项数为3;
故选C.
点评:本题考查二项式定理的应用,难点在于得到各项系数绝对值的表达式,进而由二项式定理求出M的值.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 的展开式的各项系数之和为
的展开式的各项系数之和为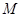 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中常数项为___________.
,则展开式中常数项为___________. 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
)
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
) 的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____
的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____ 的展开式的各项系数之和为M,二项式系数之和为N,若
的展开式的各项系数之和为M,二项式系数之和为N,若 ,则展开式中
,则展开式中 的系数为 。
的系数为 。 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )