题目内容
给出数列{an}的条件如下:①设bn=2an,{bn}是等差数列;②设bn-1=an-1+an(n≥2),{bn}是等差数列;
③前n项的和Sn=n2+1;④设bn=2an-1,数列{bn}前n项和为n2.其中使数列{an}是等差数列的条件的正确序号是 ________.
①,④
分析:①中根据,{bn}是等差数列可推断出an-an-1也是常数,进而推断出数列{an}为等差数列;②中根据数列的递推可求得an+1-an-1为常数但不是相邻的两项,故数列{an}不一定是等差数列②不正确;③根据数列的递推式可求得数列{an}的通项公式,推断出不是等差数列;④中根据2an-1=n2-(n-1)2求得数列的通项公式,进而推断出数列为等差数列.最后综合可得答案.
解答:对于①{bn}是等差数列,∴bn-bn-1=2an-2an-1=d(常数)
∴an-an-1= ,故数列{an}为等差数列,①正确.
,故数列{an}为等差数列,①正确.
∵bn-1=an-1+an,∴bn=an+an+1,两式相减得an+1-an-1=d,数列{an}不一定是等差数列②不正确
③中Sn=n2+1,∴当n≥2时,an=Sn-Sn-1=2n-1,但a1=12+1=2不符合an=2n-1
∴an= ∴数列{an}不是等差数列
∴数列{an}不是等差数列
④2an-1=n2-(n-1)2=2n-1,n≥2,an=n,当n=1时a1=1符合
∴an=n,∴数列{an}为等差数列
故答案为:①④
点评:本题主要考查了等差数列的定义和等差数列的通项公式的应用.考查了学生对等差数列的基础知识的综合运用.
分析:①中根据,{bn}是等差数列可推断出an-an-1也是常数,进而推断出数列{an}为等差数列;②中根据数列的递推可求得an+1-an-1为常数但不是相邻的两项,故数列{an}不一定是等差数列②不正确;③根据数列的递推式可求得数列{an}的通项公式,推断出不是等差数列;④中根据2an-1=n2-(n-1)2求得数列的通项公式,进而推断出数列为等差数列.最后综合可得答案.
解答:对于①{bn}是等差数列,∴bn-bn-1=2an-2an-1=d(常数)
∴an-an-1=
 ,故数列{an}为等差数列,①正确.
,故数列{an}为等差数列,①正确.∵bn-1=an-1+an,∴bn=an+an+1,两式相减得an+1-an-1=d,数列{an}不一定是等差数列②不正确
③中Sn=n2+1,∴当n≥2时,an=Sn-Sn-1=2n-1,但a1=12+1=2不符合an=2n-1
∴an=
 ∴数列{an}不是等差数列
∴数列{an}不是等差数列④2an-1=n2-(n-1)2=2n-1,n≥2,an=n,当n=1时a1=1符合
∴an=n,∴数列{an}为等差数列
故答案为:①④
点评:本题主要考查了等差数列的定义和等差数列的通项公式的应用.考查了学生对等差数列的基础知识的综合运用.

练习册系列答案
相关题目
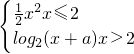 在定义域内是连续函数,数列{an}通项公式为an=
在定义域内是连续函数,数列{an}通项公式为an=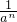 ,则数列{an}的所有项之和为1.
,则数列{an}的所有项之和为1.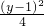 =1有唯一公共点的直线有且只有两条.
=1有唯一公共点的直线有且只有两条.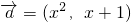 ,
,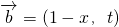 ,若函数f(x)=
,若函数f(x)= 在区间[-1,1]上是增函数,则实数t的取值范围是(5,+∞);
在区间[-1,1]上是增函数,则实数t的取值范围是(5,+∞); 在定义域内是连续函数,数列{an}通项公式为an=
在定义域内是连续函数,数列{an}通项公式为an= ,则数列{an}的所有项之和为1.
,则数列{an}的所有项之和为1.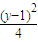 =1有唯一公共点的直线有且只有两条.
=1有唯一公共点的直线有且只有两条. ,
, ,若函数f(x)=
,若函数f(x)= 在区间[-1,1]上是增函数,则实数t的取值范围是(5,+∞);
在区间[-1,1]上是增函数,则实数t的取值范围是(5,+∞); +
+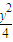 =1,直线l的方程是y=x+3.
=1,直线l的方程是y=x+3.