Question

在△ABC中，若b=1，，，则S_△ABC=　　．

Answer 1

考点：

正弦定理的应用．

专题：

计算题．

分析：

由正弦定理求出sinB的值，可得B的值，再由三角形的内角和公式 求出C的值，再由S_△ABC= 运算求得结果．

解答：

解：由于在△ABC中，若b=1，，，由正弦定理可得 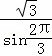=，∴sinB=．

再由大边对大角可得 B=＜A，∴C=π﹣A﹣B=．

∴则S_△ABC==，

故答案为 ．

点评：

本题主要考查正弦定理的应用，三角形的内角和公式，大边对大角，属于中档题．