题目内容
已知定义域为R的函数f(x)=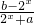 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对于任意t∈(2,3),不等式f(kt2-2t)+f(1-t)<0恒成立,求k的范围.
解:(1)∵定义域为R的函数f(x)=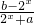 是奇函数,
是奇函数,
∴f(-x)=-f(x),即
∴
解得a=1,b=1. …(4分)
(2)由(1)知,f(x)= =-1+
=-1+
∴f(x)为R上的减函数 …(7分)
∵对于任意t∈(2,3),不等式f(kt2-2t)+f(1-t)<0恒成立,
∴f(kt2-2t)<-f(1-t)=f(t-1)
∴kt2-2t>t-1,∴k> 对于任意t∈(2,3)恒成立,
对于任意t∈(2,3)恒成立,
∵ =-
=- ,
,
∴ ∈(
∈( ,
, )
)
∴k≥ …(12分)
…(12分)
分析:(1)利用奇函数的定义,建立等式,即可求a,b的值;
(2)求得函数的单调性,将不等式化为具体不等式,利用分离参数法,即可求k的范围.
点评:本题考查函数的奇偶性,考查恒成立问题,解题的关键是确定函数的单调性,利用分离参数法,属于中档题.
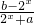 是奇函数,
是奇函数,∴f(-x)=-f(x),即

∴

解得a=1,b=1. …(4分)
(2)由(1)知,f(x)=
 =-1+
=-1+
∴f(x)为R上的减函数 …(7分)
∵对于任意t∈(2,3),不等式f(kt2-2t)+f(1-t)<0恒成立,
∴f(kt2-2t)<-f(1-t)=f(t-1)
∴kt2-2t>t-1,∴k>
 对于任意t∈(2,3)恒成立,
对于任意t∈(2,3)恒成立,∵
 =-
=- ,
,
∴
 ∈(
∈( ,
, )
)∴k≥
 …(12分)
…(12分)分析:(1)利用奇函数的定义,建立等式,即可求a,b的值;
(2)求得函数的单调性,将不等式化为具体不等式,利用分离参数法,即可求k的范围.
点评:本题考查函数的奇偶性,考查恒成立问题,解题的关键是确定函数的单调性,利用分离参数法,属于中档题.

练习册系列答案
相关题目