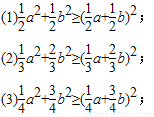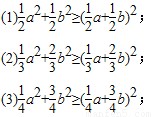Question

已知a，b∈R，可以证明：

(1) 1 2 a2+ 1 2 b2≥( 1 2 a+ 1 2 b)2； (2) 1 3 a2+ 2 3 b2≥( 1 3 a+ 2 3 b)2； (3) 1 4 a2+ 3 4 b2≥( 1 4 a+ 3 4 b)2；

根据上述不等式，写出一个更一般的结论，并加以证明．

Answer 1

分析：一般性结论为：已知a，b∈R，均为正数，若m+n=1则ma²+nb²≥（ma+nb）²，利用分析法证明即可．

解答：解：一般性结论为：已知a，b∈R，均为正数，若m+n=1则ma²+nb²≥（ma+nb）²（4分）
证明：要证ma²+nb²≥（ma+nb）²
即证ma²+nb²≥m²a²+n²b²+2mnab
即证m（1-m）a²+n（1-n）b²-2mnab≥0又m+n=1
故即证mn（a²+b²-2ab）≥0（6分）
即证mn（a-b）²≥0
因为m，n为正数（a-b）²≥0
故mn（a-b）²≥0显然成立，所以原命题成立．（8分）

点评：本题考查类比推理，考查分析法的运用，属于基础题．