题目内容
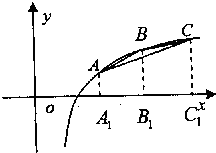 在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
(1)试比较f(m-1)+f(m+1)与2f(m)的大小;
(2)求△ABC的面积S=g(m)的值域.
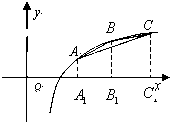 解:(1)∵f(m-1)+f(m+1)=lg(m-1)+lg(m+1)=lg(m2-1),2f(m)=2lgm=lgm2>lg(m2-1),
解:(1)∵f(m-1)+f(m+1)=lg(m-1)+lg(m+1)=lg(m2-1),2f(m)=2lgm=lgm2>lg(m2-1),∴f(m-1)+f(m+1)<2f(m).
(2)△ABC的面积S=g(m)=
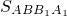 +
+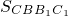 -
-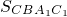
=
 [lg(m-1)+lgm]+
[lg(m-1)+lgm]+ [lg(m+1)+lgm]-
[lg(m+1)+lgm]- [lg(m-1)+lg(m+1)]×2=
[lg(m-1)+lg(m+1)]×2= lg[
lg[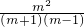 ]=
]= lg(1+
lg(1+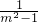 ),
),∵m>2时,S=g(m)单调递减,
∴0<S<
 lg
lg ,
,故△ABC的面积S的值域为 (0,
 lg
lg ].
].分析:(1)计算 f(m-1)+f(m+1)为 lg(m2-1),化简2f(m)为 lgm2,由此可得较f(m-1)+f(m+1)与2f(m)的大小关系.
(2)根据△ABC的面积S=g(m)=
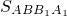 +
+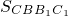 -
-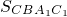 ,化简为
,化简为 lg(1+
lg(1+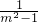 ),再根据m>2时,S=g(m)单调递减求得△ABC的面积S的值域.
),再根据m>2时,S=g(m)单调递减求得△ABC的面积S的值域.点评:本题主要考查对数值大小的比较,对数函数的图象和性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设f(x)=1g(
+a)是奇函数,且在x=0处有意义,则该函数是( )
| 2 |
| 1-x |
| A、(-∞,+∞)上的减函数 |
| B、(-∞,+∞)上的增函数 |
| C、(-1,1)上的减函数 |
| D、(-1,1)上的增函数 |
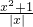 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题: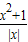 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题: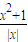 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题: