题目内容
函数 ,其中
,其中 为实常数。
为实常数。
(1)讨论 的单调性;
的单调性;
(2)不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)若 ,设
,设 ,
,
 。是否存在实常数
。是否存在实常数 ,既使
,既使 又使
又使 对一切
对一切 恒成立?若存在,试找出
恒成立?若存在,试找出 的一个值,并证明;若不存在,说明理由.
的一个值,并证明;若不存在,说明理由.
(1)当 时,增区间为
时,增区间为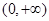 ,无减区间;当
,无减区间;当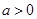 时,增区间为
时,增区间为 ,减区间为
,减区间为 ;(2)
;(2) ;(3)存在,如
;(3)存在,如 等,证明见详解.
等,证明见详解.
解析试题分析:(1)首先求导函数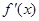 ,然后对参数
,然后对参数 进行分类讨论
进行分类讨论 的单调性;(2)根据函数的解析式可将问题转化为
的单调性;(2)根据函数的解析式可将问题转化为 的最大值,再利用导数研究函数单调性来确定其最值;(3)假设存在,将问题转化为证明:
的最大值,再利用导数研究函数单调性来确定其最值;(3)假设存在,将问题转化为证明: 及
及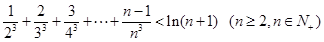 成立,然后可考虑综合法与分析法进行证明.
成立,然后可考虑综合法与分析法进行证明.
试题解析:(1)定义域为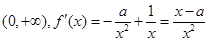 ,
,
①当 时,
时, ,
,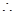
 在定义域
在定义域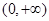 上单增;
上单增;
②当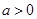 时,当
时,当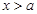 时,
时, ,
, 单增;当
单增;当 时,
时, ,
, 单减.
单减.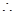 增区间:
增区间: ,减区间:
,减区间: .
.
综上可知:当 时,增区间
时,增区间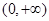 ,无减区间;当
,无减区间;当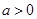 时,增区间:
时,增区间: ,减区间:
,减区间: .
.
(2) 对任意
对任意 恒成立
恒成立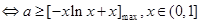 ,令
,令 ,
, ,
,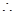
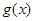 在
在 上单增,
上单增,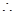
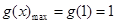 ,
,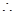
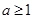 ,故
,故 的取值范围为
的取值范围为 .
.
(3)存在,如 等.下面证明:
等.下面证明:
及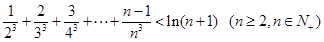 成立.
成立.
①先证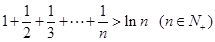 ,注意
,注意 ,
,
这只要证 (*)即可,
(*)即可,
容易证明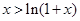 对
对 恒成立(这里证略),取
恒成立(这里证略),取 即可得上式成立.
即可得上式成立.
让 分别代入(*)式再相加即证:
分别代入(*)式再相加即证: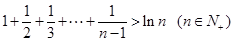 ,
,
于是 .
.
②再证 ,
,
法一: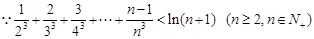

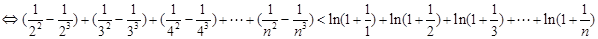
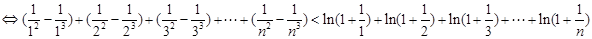 ,
,
只须证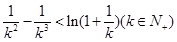 ,构造证明函数不等式:
,构造证明函数不等式: ,
,
令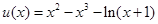 ,
,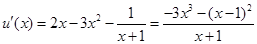 ,
,
当 时,
时, 在
在 上单调递减,
上单调递减,
又
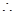 当
当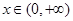 时,恒有
时,恒有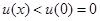 ,即
,即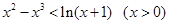 恒成立.
恒成立. ,取
,取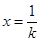 ,则有
,则有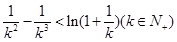 ,
,
让 分别代入上式再相加即证:
分别代入上式再相加即证: ,
,
即证
练习册系列答案
相关题目
 .
. x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0. (a为常数).
(a为常数).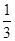 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.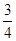 x2-bx+
x2-bx+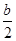 -
-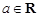 ,函数
,函数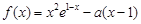 .
.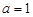 时,求
时,求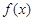 在
在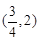 内的极大值;
内的极大值;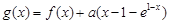 ,当
,当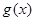 有两个极值点
有两个极值点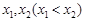 时,总有
时,总有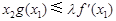 ,求实数
,求实数 的值.(其中
的值.(其中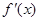 是
是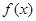 的导函数.)
的导函数.)