题目内容
以下说法中正确的是
(1){x|x2-x+1=0,x∈R}是空集
(2)任何一个集合必有两个子集
(3)x2+1=2x的解可表示为{1,1};
(4)集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合.
(1)
(1)
.(1){x|x2-x+1=0,x∈R}是空集
(2)任何一个集合必有两个子集
(3)x2+1=2x的解可表示为{1,1};
(4)集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合.
分析:对于(1):利用空集的意义结合一元二次方程根的情况进行判断;(2)利用集合的子集与真子集的定义,直接判断;(3)根据集合中元素的性质进行判断;集合{y|y=x2-1}表示函数的值域,集合{(x,y)|y=x2-1}表示函数图象上的点集,据此对(4)进行判断.
解答:解:对于(1),x2-x+1=0的根的判别式△=-3<0,则此方程没有实数根,故){x|x2-x+1=0,x∈R}是空集,正确;
对于(2),任何一个集合必有两个子集,不正确,因为集合是∅没有两个子集;
对于(3),x2+1=2x的解是x1=x2=1,可表示为{1},故(3)错;
对于(4),集合{y|y=x2-1}表示函数的值域;集合{(x,y)|y=x2-1}表示函数图象上的点集,不是同一个集合,故(4)不正确;
故答案为:(1).
对于(2),任何一个集合必有两个子集,不正确,因为集合是∅没有两个子集;
对于(3),x2+1=2x的解是x1=x2=1,可表示为{1},故(3)错;
对于(4),集合{y|y=x2-1}表示函数的值域;集合{(x,y)|y=x2-1}表示函数图象上的点集,不是同一个集合,故(4)不正确;
故答案为:(1).
点评:本题考查命题真假的判定,考查空集、集合的含义,考查集合中元素的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的线性相关关系时,发现两个人对
的线性相关关系时,发现两个人对 的观测数据的平均值相等,都是
的观测数据的平均值相等,都是 。对
。对 的观测数据的平均值也相等,都是
的观测数据的平均值也相等,都是 。各自求出的回归直线分别是
。各自求出的回归直线分别是 ,则直线
,则直线 。
。 的值越大,说明“
的值越大,说明“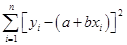 最小。
最小。 来刻画回归效果,
来刻画回归效果, A、直线的倾斜角为锐角,在x轴与y轴上的截距都为正
A、直线的倾斜角为锐角,在x轴与y轴上的截距都为正 C、直线斜率小于0,在x轴与y轴上的截距是一正一负
C、直线斜率小于0,在x轴与y轴上的截距是一正一负