题目内容
(文科做)已知曲线f(x)=x3+bx2+cx+d经过原点(0,0),且直线y=0与y=-x均与曲线c:y=f(x)相切.(1)求f(x)的解析式;
(2)在b∈R+时,求函数y=f(x)的极值.
【答案】分析:(1)易得出d=0,y=x3+bx2+cx.设y=-x与y=x3+bx2+cx切于点(x,y),则有如下三个关系:①点(x,y)在y=-x上,②点(x,y)在y=x3+bx2+cx上 ③f′(x)=-1
以x0为桥梁得出b,c关系或数值.同样地再通过y=-x均与曲线c:y=f(x)相切.最后确定b,c的值,得出解析式.
(2)利用函数导数与单调性的关系,求出的单调区间,再求极值.
解答:解:(1)若y=x3+bx2+cx+d过点(0,0),则d=0,∴y=x3+bx2+cx.
设y=-x与y=x3+bx2+cx切于点(x,y),则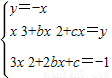 即
即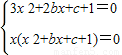 ,
,
若x=0时,则c+1=0;
若x≠0时,则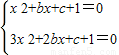 则2x2+bx=0,∵x≠0,,则有
则2x2+bx=0,∵x≠0,,则有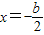 ,将
,将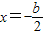 代入x2+bx+c+1=0中得到:
代入x2+bx+c+1=0中得到: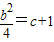 .
.
故c=-1或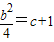 .
.
设y=0与y=x3+bx2+cx切于点(x1,y1),则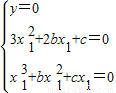 ,即
,即 ,
,
若x1=0时,有c=0;
若x1≠0时,则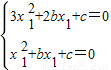 则2x12+bx1=0,∴
则2x12+bx1=0,∴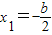 代3x12+2bx1+c=0中得到
代3x12+2bx1+c=0中得到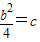
故c=0或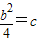 .
.
在c=-1时,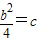 不可能成立,舍c=-1.
不可能成立,舍c=-1.
在c=0时,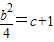 ,则b=±2,故所是解析式为y=x3±2x2.
,则b=±2,故所是解析式为y=x3±2x2.
(2)在b>0时,y=x3+2x2,y′=3x2+4x=x(3x+4)
由y′>0得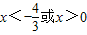 f(x)的单增区间是(-∞,
f(x)的单增区间是(-∞,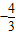 ),(0,+∞)
),(0,+∞)
由y′=0 得x=- 或x=0
或x=0
由y′<0得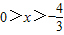 ,f(x)的单减区间是(
,f(x)的单减区间是(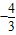 ,0)
,0)
在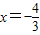 时取极大值.
时取极大值.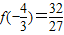 ,x=0时取得极小值 f(0)=0
,x=0时取得极小值 f(0)=0
点评:本题考查导数的几何意义,函数导数与单调性的关系,函数极值求解,是常规题.
以x0为桥梁得出b,c关系或数值.同样地再通过y=-x均与曲线c:y=f(x)相切.最后确定b,c的值,得出解析式.
(2)利用函数导数与单调性的关系,求出的单调区间,再求极值.
解答:解:(1)若y=x3+bx2+cx+d过点(0,0),则d=0,∴y=x3+bx2+cx.
设y=-x与y=x3+bx2+cx切于点(x,y),则
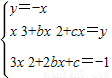 即
即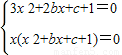 ,
,若x=0时,则c+1=0;
若x≠0时,则
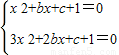 则2x2+bx=0,∵x≠0,,则有
则2x2+bx=0,∵x≠0,,则有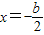 ,将
,将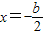 代入x2+bx+c+1=0中得到:
代入x2+bx+c+1=0中得到: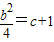 .
.故c=-1或
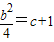 .
.设y=0与y=x3+bx2+cx切于点(x1,y1),则
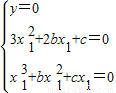 ,即
,即 ,
,若x1=0时,有c=0;
若x1≠0时,则
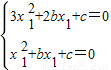 则2x12+bx1=0,∴
则2x12+bx1=0,∴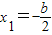 代3x12+2bx1+c=0中得到
代3x12+2bx1+c=0中得到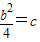
故c=0或
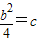 .
.在c=-1时,
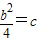 不可能成立,舍c=-1.
不可能成立,舍c=-1.在c=0时,
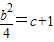 ,则b=±2,故所是解析式为y=x3±2x2.
,则b=±2,故所是解析式为y=x3±2x2.(2)在b>0时,y=x3+2x2,y′=3x2+4x=x(3x+4)
由y′>0得
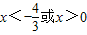 f(x)的单增区间是(-∞,
f(x)的单增区间是(-∞,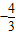 ),(0,+∞)
),(0,+∞)由y′=0 得x=-
 或x=0
或x=0由y′<0得
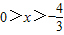 ,f(x)的单减区间是(
,f(x)的单减区间是(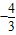 ,0)
,0)在
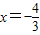 时取极大值.
时取极大值.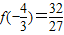 ,x=0时取得极小值 f(0)=0
,x=0时取得极小值 f(0)=0点评:本题考查导数的几何意义,函数导数与单调性的关系,函数极值求解,是常规题.

练习册系列答案
相关题目