题目内容
已知向量a＝(cos
x，sinx)，b＝(
)，且x∈[0，
]．若f(x)＝a·b－2
｜a＋b｜的最小值是
，求
的值．
答案：
解析：
解析：
|
解：a·b |a＋b|
①若 ②若0≤ 由已知得 ③若 |
∴cosx≥0，因此|a＋b|＝2cosx
｜a＋b｜即
＜0，则当且仅当cosx＝0时，f(x)取得最小值－1，这与已知矛盾；
≤1，则当且仅当cosx＝
，
，解得：
，
，解得：
，这与
相矛盾．
为所求．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
，－1)，则|2a－b|的最大值、最小值分别是________．
，－1)，则|2a－b|的最大值是________．
.
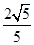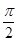<β<0<α<
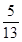，求sinα的值．