题目内容
已知函数f(x)=lnx,g(x)= (a>0),设h(x)=f(x)+g(x),
(a>0),设h(x)=f(x)+g(x),
(Ⅰ)求h(x)的单调区间;
(Ⅱ)若在y=h(x)在x∈(0,3]的图象上存在一点P(x0,y0),使得以P(x0,y0)为切点的切线的斜率k≥ 成立,求实数a的最大值;
成立,求实数a的最大值;
(Ⅲ)是否存在实数m,使得函数y=g( )+m-1的图象于y=f(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由。
)+m-1的图象于y=f(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由。
 (a>0),设h(x)=f(x)+g(x),
(a>0),设h(x)=f(x)+g(x),(Ⅰ)求h(x)的单调区间;
(Ⅱ)若在y=h(x)在x∈(0,3]的图象上存在一点P(x0,y0),使得以P(x0,y0)为切点的切线的斜率k≥
 成立,求实数a的最大值;
成立,求实数a的最大值;(Ⅲ)是否存在实数m,使得函数y=g(
 )+m-1的图象于y=f(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由。
)+m-1的图象于y=f(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由。 解:(Ⅰ)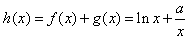 ,其定义域为(0,+∞),
,其定义域为(0,+∞),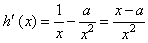 ,
,
令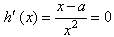 ,则x=a,
,则x=a,
于是,当x>a时,h′(x)>0,h(x)为增函数,
当0<x<a时,h′(x)<0,h(x)为减函数,
所以h(x)的单调增区间是(a,+∞),单调减区间是(0,a);
(Ⅱ)因为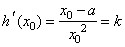 ,
,
所以在区间x∈(0,3]上存在一点P(x0,y0),
使得以P(x0,y0)为切点的切线的斜率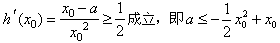 ,
,
等价于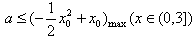 ,
,
因为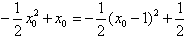 ,
,
所以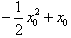 在x∈(0,3]的最大值为
在x∈(0,3]的最大值为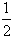 ,
,
于是a≤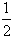 ,a的最大值为
,a的最大值为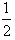 。
。
(Ⅲ)若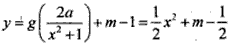 的图象与
的图象与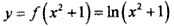 的图象恰好有四个不同的交点,
的图象恰好有四个不同的交点,
即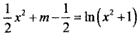 有四个不同的根,亦即方程
有四个不同的根,亦即方程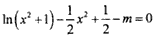 有四个不同的根。
有四个不同的根。
构造函数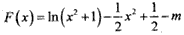 ,
,
则F(x)的图象与x轴有四个不同的交点,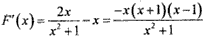 ,
,
令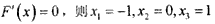 ,
,
当x变化时F′(x)和F(x)的变化情况如下表: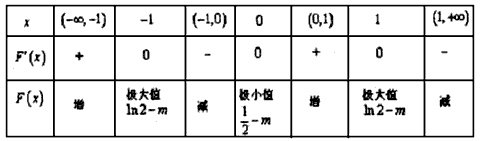
所以当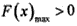 且
且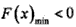 即
即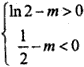 时,F(x)的图象与x轴有四个不同的交点,
时,F(x)的图象与x轴有四个不同的交点,
解得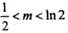 ,
,
所以存在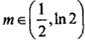 使得两个函数的图像恰好有四个不同的交点。
使得两个函数的图像恰好有四个不同的交点。

练习册系列答案
相关题目