Question

定义：若数列{A_n}满足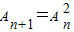则称数列{A_n}为“平方递推数列”，已知数列{a_n}中，a₁=2，点{a_n，a_n+1}在函数f（x）=2x²+2x的图象上，其中n的正整数．
（1）证明数列{2a_n+1}是“平方递推数列”，且数列{lg（2a_n+1）}为等比数列；
（2）设（1）中“平方递推数列”的前n项之积为T_n，即T_n=（2a₁+1）（2a₂+1）…（2a_n+1），求数列{a_n}的通项及T_n关于n的表达式；
（3）记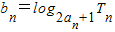，求数列{b_n}的前n项和S_n，并求使S_n＞2008的n的最小值．

Answer 1

【答案】分析：（Ⅰ）由a_n+1=2a_n²+2a_n，a_n＞0，知2a_n+1+1=4a_n²+4a_n+1=（2a_n+1）²，所以{2a_n+1}是“平方递推数列”．由lg（2a_n+1+1）=2lg（2a_n+1），且2a_n+1＞1，知lg（1+2a_n）＞0，由此能够证明{lg（2a_n+1）}为等比数列．
（Ⅱ）由lg（2a₁+1）=lg5，知lg（2a_n+1）=lg5•2^n-1，所以，由lgT_n=lg（2a₁+1）+lg（2a₂+1）+…+lg（2a_n+1）=，能求出T_n．
（Ⅲ）由，知==由此能求出n的最小值．
解答：证明：（Ⅰ）由条件得：a_n+1=2a_n²+2a_n，a_n＞0．
∴2a_n+1+1=4a_n²+4a_n+1=（2a_n+1）²，
∴{2a_n+1}是“平方递推数列”．
由lg（2a_n+1+1）=2lg（2a_n+1），
且2a_n+1＞1，
∴lg（1+2a_n）＞0，
∴，
∴{lg（2a_n+1）}为等比数列．…（3分）
解：（Ⅱ）∵lg（2a₁+1）=lg5，
∴lg（2a_n+1）=lg5•2^n-1，
∴
∴…（5分）
∵lgT_n=lg（2a₁+1）+lg（2a₂+1）+…+lg（2a_n+1），
=，
∴…（7分）
（Ⅲ），
∴
=
=．…（10分）
由S_n＞2008，得2n-2+2＞2008，n+（）ⁿ＞1005，
当n≤1004时，n+（）ⁿ＜1005，当n≥1005时，n+（）ⁿ＞1005，
∴n的最小值为1005．…（13分）
点评：本题首先考查等差数列、等比数列的基本量、通项，结合含两个变量的不等式的处理问题，考查对新定义的理解能力．本题将数列放到新情境中，关键是正确理解题意，挖掘问题的本质与隐含．