题目内容
在 中,
中, 为
为 的对边,且
的对边,且 ,则( )
,则( )
A. 成等差数列 成等差数列 | B. 成等差数列 成等差数列 |
C. 成等比数列 成等比数列 | D. 成等比数列 成等比数列 |
D
解析试题分析:因为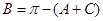 ,所以
,所以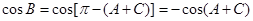 ,且由二倍角公式可得
,且由二倍角公式可得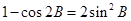 ,所以
,所以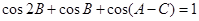 可化为
可化为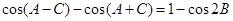 即
即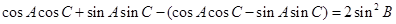 也就是
也就是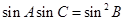 ,根据正弦定理可得
,根据正弦定理可得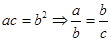 ,所以
,所以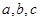 成等比数列,选D.
成等比数列,选D.
考点:1.两角和差公式;2.二倍角公式;3.正弦定理;4.等比数列的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设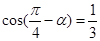 ,则
,则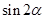 =( )
=( )
A.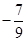 | B.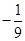 | C.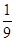 | D.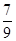 |
已知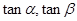 是方程
是方程 的两根,且
的两根,且 ,则
,则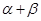 等于( )
等于( )
A. | B. | C. | D. |
已知tan(α+β)= ,tan(α+
,tan(α+ )=
)= , 那么tan(β-
, 那么tan(β- )的值是( )
)的值是( )
A. | B. | C. | D. |

 = ( )
= ( )
A.- | B.- | C. | D. |
设 与
与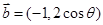 垂直,则
垂直,则 的值等于
的值等于
A. | B. | C.0 | D.-l |
在△ABC中,若tanAtanB=tanA+tanB+1,则cosC的值是( )
A.- | B. | C. | D.- |
[2014·太原模拟]已知锐角α,β满足sinα=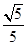 ,cosβ=
,cosβ=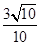 ,则α+β等于( )
,则α+β等于( )
A.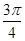 | B. 或 或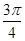 |
C. | D.2kπ+ (k∈Z) (k∈Z) |
 MGA=a(
MGA=a(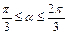 ).
). 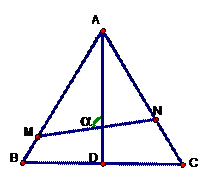
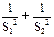 的最大值与最小值.
的最大值与最小值.